サル用ターゲット探索課題を学習可能な動的状態空間付き強化学習モデル:経験飽和度と決定一意性に基づく状態の自己決定
東北医科薬科大学医学部
坂本 一寛
Katakura, T., Yoshida, M., Hisano, H., Mushiake, H. and Sakamoto, K.
Reinforcement learning model with dynamic state space tested on target search tasks for monkeys: self-determination of previous states based on experience saturation and decision uniqueness.
Front. Comput. Neurosci., 15: 784592 (2022). doi: 10.3389/fncom.2021.784592
https://www.frontiersin.org/articles/10.3389/fncom.2021.784592/
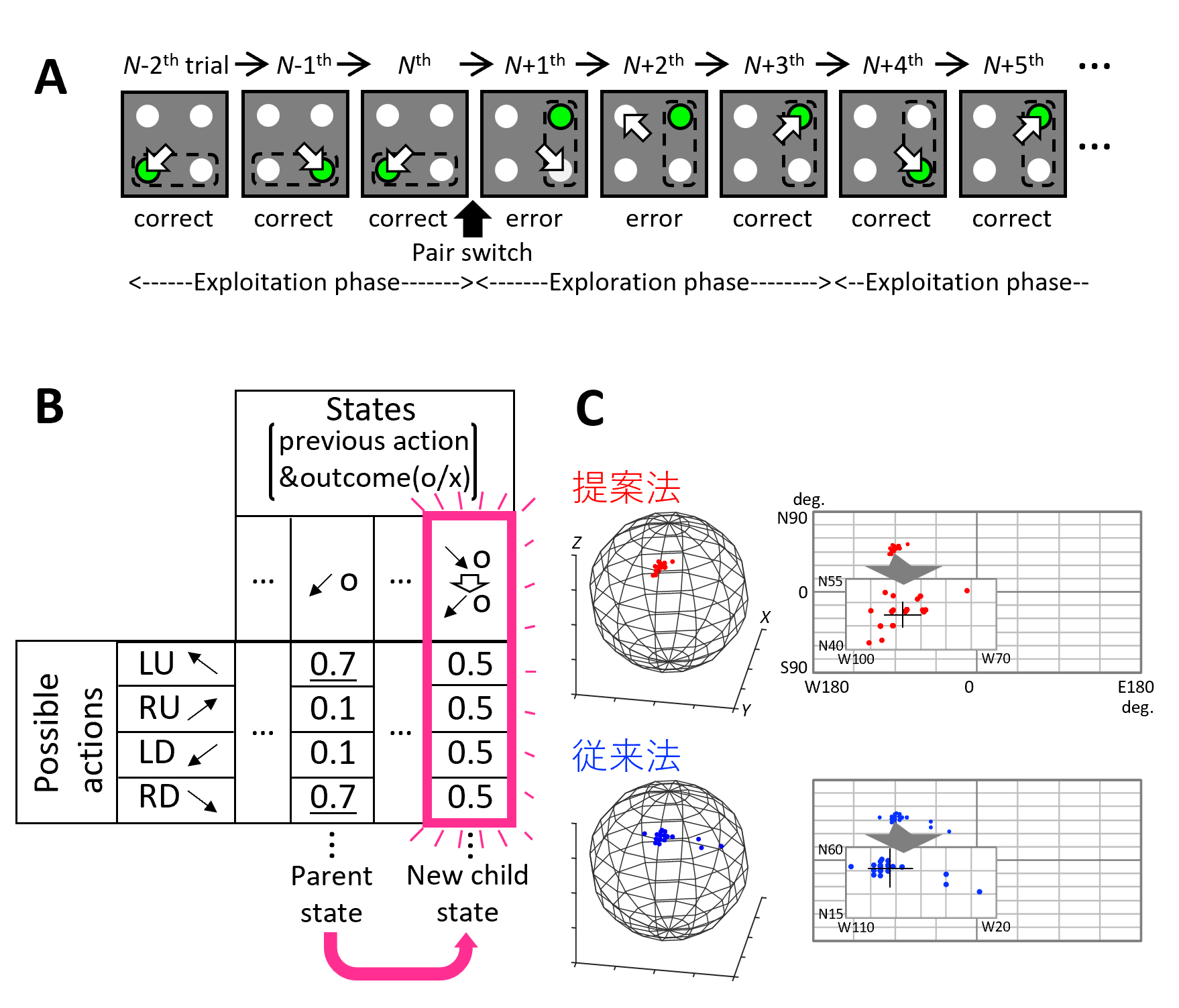
本論文では、我々が以前サルに用いた2ターゲット探索課題(図1A, Kawaguchi et al., JNP 2015)を学習可能な理論モデルを提案しました。
課題では、被験者が固視点を固視しているとその周囲に4つの光点が提示され、その中に隠れた正解ターゲットを見ると報酬が与えられます。ある期間では隣接2点ペアが交互に正解ターゲットとなり、その後、7試行連続正解すると、被験者には知らされず別のペアが正解ターゲットになります。
強化学習では、報酬が最も得られるようにどう行動すべきかを学習します。マルコフ性が仮定される、つまり、ある時刻の状態sから次の時刻における行動が決定されます。本モデルでは、行動価値関数Q(ai, t)を考え、各状態、各行動に対してQ値を持たせます。Q値の“一覧表”はQテーブルと言います。
通常の強化学習では、状態sは事前知識ないしは一定時間刻みとしてモデル作成者が規定します。しかしながら、2ターゲット探索課題を学習するのに、1試行を1つの時間ステップないしは1つの状態として強化学習モデルに作りつけるのでは、サルのような高い正答率は得られません。なぜならば、1つ前の試行の行動と正誤だけからは、行動を一意に決定できないからです(例えば、図1Bの例の“1試行前に左下ターゲットを見て正解した”状態では、右下ないしは左上ターゲットを見るという二択止まり)。
この課題で、状態sを事前知識としてモデル作成者が規定することなく、高い正答率を得ようとするならば、状態・確率空間そのものもモデル自身が規定する必要があります。つまり、モデル自ら直近2試行を1つ前の状態と規定しながら、行動選択する必要があるのです。モデルは実際、1試行前の行動と結果に基づき行動選択することから始めますが、それでは、図1Bのように二択状態以上に学習は進みません。そこで“これ以上試行を経験してもQ値は大きく変動しない”という経験飽和度という新たな基準が満たされた場合、Qテーブルが行動を一意に決定できるものになっているか(決定一意性)を判定し、できない場合はもう一試行遡り、新たな状態を生成するようにしました。
詳細は略しますが、本モデルは2ターゲット探索課題を高い正答率で学習しただけでなく、モデルが本来想定していない本課題変形版も学習することができました。想定していない課題に対する学習能は、本モデルの特筆すべきところです。本モデルは更に各課題イベントにおける行動(例えば、遅延期間は固視を続ける等)も学習できるよう拡張されました(Sakamoto et al., 2022)。
研究は遅々としていますが、ご支援いただいたイメージングにより齧歯類で2ターゲット探索課題遂行中の脳活動を計測すべく、高精度のマウス用ヴァーチャルリアリティシステムも提案しました(図1C, Zuguchi et al., 2023)。これらにより理論と実験の包括システムを構築し、高次脳機能の神経基盤を解明していきたいと願っています。
図1. 2ターゲット探索課題を用いた理論・実験の包括システム。
(A)課題における正解ターゲットペア切り替え例。
(B)動的状態空間付き強化学習モデルにおけるQテーブル拡張の模式図。
(C)マウス用ヴァーチャルリアリティシステムの球体トレッドミルの回転軸を精度よく推定する手法を提案。