第7章:パラメトリック検定
ナレーション原稿
パラメトリック検定についてですが、代表的なのが2つのグループの平均の差の検定、平均値に違いがあるかどうかの検定というものです。午前中にちょっと出てきた労働時間ですね。何となく男性のほうが長そうだなというのが分かって、これはただ標本調査から得られたデータなので、日本人を対象に抽出してやった調査の結果なんですが、じゃあ、これが本当に母集団である日本人で、本当に一般的に当てはまることなのかというのを検定してあげるがt検定というものです。
t検定には3種類あって、比較するデータに対応がない場合に使われる。対応がないというのは、だいたい判断する基準としては同じ人からデータを取っているか、取っていないかで判断できます。対応がある場合は同じ人に2回取ったときに対応のあるt検定を使います。なので、対応のあるt検定は基本的には縦断データです。何回も同じ人の状態を調査するような調査だったり、実験とか、そういうので使われます。
普通の横断研究では基本的にはこっちの2つです。スチューデントのt検定とウェルチのt検定。違いは何かというと、2つの群、この場合だと男性と女性で労働時間のばらつきが等しいと見なせるか見なせないかで使い分けをします。ただ、ウェルチのt検定のほうが広い、つまり分散が等しかろうが、等しくなかろうが使えて、最近はどうやら最初からウェルチのt検定をやってしまえという人も増えてきているところです。ただ、ソフトによって結構違っていて、SPSSとかそういうのは、まず分散が等しいか、等しくないかという検定の結果を出してくれた上でウェルチのt検定とスチューデントのt検定の結果を出してくれるというソフトもあるので、そういう場合は選んで、分散が等しいと見なせるかどうかの検定をまず見て、等しくないとなったらウェルチのt検定の結果を採用する。等しいと見なせる場合スチューデントのt検定の結果を採用するというやり方をする人もいます。
2通り考え方があって、先に分散が等しいと見なせるか見なせないかというのを調べた上でどっちを適用かするかというのを考える一派と、どっちも含んでいるんだったらウェルチのt検定でいいじゃないか、面倒くさいから。2回も検定してするのは嫌だよという人はt検定。ウェルチのt検定を先に使う、全部ウェルチのt検定だという考え方の人は、検定は繰り返せば繰り返すほど何回も何回もやるとどんどん、どこかで有意になってしまう確率が、後で出てきますが、どこかで差があると、少なくとも1回は差があるというふうになってしまう確率が上がってしまうので、検定をあまり繰り返したくないという人は最初からウェルチのt検定を使ってやってしまう。ただ、今からちょっと出てきますが、ウェルチのt検定のほうがちょっと計算が複雑です。ですが、今はコンピュータが計算してくれるので、最初からウェルチのt検定で僕はいいのではないかと思っているかもしれないですが、こういう計算です。t値というのを、これがさっき検定の原理に使った検定統計量というものですね。t値はこういう計算式で計算できます。この検定統計量t、t値というのは自由度、全体のサンプル数、標本数、対象数から2を引いた自由度を持ったt分布に従うということが分かっています。
なので、tという値を出してあげて、自由度、これだけのt分布でこの値が得られる確率を出してあげよう。出してあげて、その確率を見て、5%より上か下かというのを見て、差があるかどうかという結論を出すという話ですね。
さっきの労働時間の例でいうと、このt値は計算すると22.461という値になりました。自由度は度数が1144+957-2なので2099。自由度2099のt分布で22.461というt値が得られる確率は1.32×10-100、つまり、0.00000、バーッと0が続いて132。つまりものすごいレアな確率ということで、つまり、この場合、帰無仮説は男性と女性で労働時間の平均値が同じかという帰無仮説を立てたんですが、その仮定のもと、このデータ、こういうデータが得られる確率を計算してあげると、ものすごくあり得ないということが分かってくる。
じゃあ、そんなにあり得ないことが起きてしまうのは、もともとの仮定が間違っていたではないか。つまり帰無仮説、男性と女性の労働時間が同じというのは間違い。すなわち、男性と女性で労働時間が違うと考えたほうが合理的だよねというのがこの流れですね。
同じようにウェルチのt検定というのでは労働時間のばらつきは違いがあると仮定しているときにやるわけで、さらにこの計算式が複雑になっているんですが、tというのは自由度、νのt分布に従うということが分かっています。
これに従って計算してあげると、tが23.57122、自由度が2038.703。この場合小数点以下で切り捨てて分布表を見るというルールになっているので、自由度2038のt分布で、tが23.57122となる確率はさっきと同じです。3.9×10-109ということで、0.00000、0がバーッと続いて390ということで、これまたものすごく起こりづらい現象だということになります。
平均の差の検定で、2グループ間で平均が違うかどうかというのを見るのはスチューデントのt検定とウェルチのt検定があるということを覚えておいてください。
さらに、グループが3グルーブになったらどうするの。男女だけではなくて、3グループ以上あるときはどうするのかというときに使うのが一元配の分散分析というものです。実は、これは3グループなくてもいいんです。2グループでも分散分析は使えるんですが、3グループ以上でも、つまり、nグループですね。何グループかあるものの平均値を比較するときに使うのが分散分析というものです。
考え方としてはばらつきに注目をします。ばらつきというのは午前中にやりましたが分散です。平均からの距離の二乗の和です。ばらつき、ある従属変数のばらつきをグループに分けることで説明できるものとグループでは説明できないばらつきに分けてあります。グループで説明できるばらつきというのが、それで説明できないばらつきに比べて大きかったら、グループ分けをすることでその変数のばらつきを説明できるということなので、そのグループ分けがある変数に影響していると考えるという考え方です。
分散分析でも同じように、さっきのt検定と同じように検定統計量を計算します。それがこのF値というものです。こんな感じで計算してあげてF値を出してあげると、このF値が自由度、グループ数-1、ケース数、全体のサンプル数-グループ数という自由度を2つというか、二次元あるんですが、この自由度のF分布に従うということが分かっています。それをもとに計算してあげる。
この場合は、データは血圧と喫煙習慣という形で、こんなデータが得られたときに血圧が3つの喫煙習慣群によって違うかどうかというのを見てあげる。出した結果はこんな感じですね。グループ間というのがグループで説明できる。グループ内というのは、グループで説明できないばらつきというものです。これが比というのはF値というもので53.980です。F分布で53.980という値が得られる確率はものすごく低い。ということなので、喫煙習慣によって血圧というのが違うよということが分かるということです。
3グループ以上になってくると問題になってくるのは多重比較というものになってきます。3つの群で平均が違うよというところまでは一元配置の3グループで分かります。ただ、どのグループとグループで差があるかというのが分散分析からでは分からない。例えばさっきの喫煙と血圧の例でいうと、たばこを吸っていない人と19本以内の人で差があるのか。それともたばこを吸っていないと20本以上の人の間で血圧に差があるのか。それとも、19本以内の人と20本以上吸っている人で血圧に差があるのかというのが分からない。
なので、そこまで知りたいというときは、それぞれのペアごとにt検定です。さっき出てきたスチューデントt検定かウェルチのt検定か。分散分析の多重比較の場合はたぶんスチューデントのt検定のもとにやるんですが、t検定を3回繰り返します。それぞれのペアについて非喫煙と19本以内の血圧の差の検定、非喫煙と20本以上の喫煙と血圧のt検定、やり方に従ったt検定。19本以内と20本以上でt検定。3回やります。
それぞれで非喫煙と19本以内の血圧に差があるか。非喫煙と20本以上で差があるか。19本以内と20本以上で差があるかという結果が出てきます。ただ、そこで注意しなければいけないのは検定の多重性の問題ということです。これは1回の検定で5%、どんなやり方でやっても5%は偶然に差が出てしまう。つまり3回繰り返すと0.95×0.95×0.95で86%の確率で有意差が出ないということなので、逆をいうと、3回やれば、何もしなくても14%の確率でどこかで、どれかは本当に差がなかったとしても差が出てしまう。これはもともと設定していた5%がだいぶ大きくなってしまっています。つまり、検定を繰り返せば繰り返すほど、偶然どこかで有意差が出てしまう確率が上がってしまうんですね。それを調整するためにやるのが多重比較の調整です。これをしないとどんどん、10回検定したら、もっと、どこかは偶然に有意になってしまうというのが出てきてしまうので、検定の回数と検定の結果、有意確率を調整してあげようという考え方が必要になってきます。これが多重比較の調整というものです。
一番シンプルなのはボンフェローニ法というもので、検定を行った回数だけ検出力が甘くなってしまうので、有意水準というのを回数で割った値。検定の回数で割った値というのを新たな有意水準に設定してあげようというのが、このボンフェローニ法の考え方です。なので、普段は0.05というのを有意水準にしているんですが、3回検定が繰り返される場合は3で割ってあげて、0.017を下回らないと有意ではないよと決めてあげます。
もしくは、逆に出てきた有意確率を3倍してあげる。どっちも意味としては同じなので、そういうふうにするソフトというか、あれもあります。こういう形で有意水準の結果が検定を何回繰り返しても一定に、5%に保たれるようにしてあげようという考え方がこの多重比較の調整ということです。
ほかにもいろいろな多重比較の調整法があるので、こちらはきょうは詳しくは触れませんが、それぞれ皆さんの研究で使う調整法が違ってきたりとか、ふさわしいものが違ってきたりとかもしますので、それは必要になったときに調べてみてください。
統計講義動画
- 第1章 イントロダクション:データの作り方
- 第2章 記述統計と推測統計、データの型
- 第3章 1変量の集計
- 第4章 2変量の集計
- 第5章 推定と検定
- 第6章 パラメトリック検定とノンパラメトリック検定
- 第7章 パラメトリック検定
- 第8章 ノンパラメトリック検定
- 第9章 重回帰分析その1多変量解析の基礎
- 第10章 重回帰分析その2回帰分析の多変量バージョン重回帰分析
- 第11章 重回帰分析その3重回帰分析の応用
- 第12章 因子分析その1尺度による潜在変数の測定
- 第13章 因子分析その2探索的因子分析の基礎
- 第14章 因子分析その3因子の回転と解釈
- 第15章 多変量解析 ロジスティック回帰分析
- 第16章 多変量解析 構造方程式モデリング
統計コンテンツクイズ
以下の表は全校生徒が300人のある高校の生徒のうち、10人を無作為に選び、各人の勉強時間と試験の得点をまとめたものである。
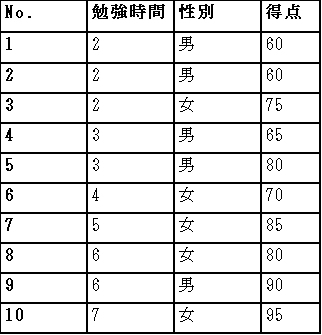
設問 7-1-1
男女で得点に差があるか検定をしたい。最も適切な検定はどれか
得点は間隔尺度で性別は名義尺度。性別は2カテゴリで対応がないのでウェルチのt検定が適切。
設問 7-1-2
男女で得点に差があるか検定を行った結果、表2のようになった。この結果の解釈として正しいのはどれか。ただし、有意水準は両側5%とする。
表2

平均値は女性の方が高いが、検定の結果を見ると、t値=-1.355でP値は0.213。P値が5%(0.05)より大きいので有意な差はないと考えられる。
設問 7-1-3
勉強時間が2時間以下の人を「短時間群」、3~4時間の人を「中時間群」、5時間以上の人を「長時間群」と3群に分けて、勉強時間と得点の関連性を検定する場合、最も適切な検定はどれか。
得点は間隔尺度で勉強時間3群は順序尺度。勉強時間3群は3カテゴリで対応がないので一元配置分散分析が適切。
設問 7-1-4
勉強時間と得点に関連があるか検定を行った結果、表3のようになった。この結果の解釈として正しいのはどれか。
表3
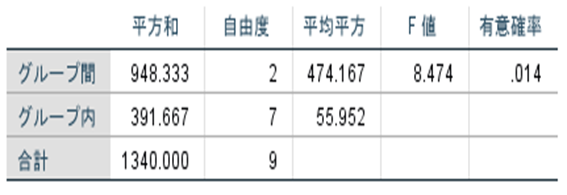
検定の結果を見ると、F値=8.474でP値は0.014。P値が5%(0.05)より小さいので有意な関連があると考えられる。