第4章:2変量の集計
ナレーション原稿
ここからは変数と変数。つまり登場人物というか登場をする変数が増えてきます。
まず、変数と変数の関連性というところですが、関連性があるということ、関連性がないということ、こういう解析をするときにどういうふうに定義をするかということです。風が吹けば桶屋がもうかるとか、そういうのと似ているというか、それをやろうとしているんです。例えば肺がんと喫煙、これは本当によく疫学で出てくる例だと思うんですが、関連性があるということは、ある変数の分布というのがほかの変数の分布の影響を受けますよ。受けていたらと関連がある可能性がある。因果とはまたちょっと違うんですが、ひとまず関連性があるというふうに定義します。例えばこの場合、喫煙をしている人が1,000人いて、1,000人中の100人が肺がんになりました。喫煙をしていなかった人も1,000人いて、10人が肺がんになりました。この場合、喫煙をしているか、していないかで肺がんを発症する人の割合が違うので、肺がんと喫煙の間には何かしらの関係があるのではないかというふうに考える。関連性があるのではないかというふうに考えると。こっちが関連性がある例です。
逆に関連性がないということは、ある変数の分布がほかの変数の影響を受けていないというふうに定義することができます。例えばいまどき携帯を持っている人、ほぼ全員が持っていると思うんですが、男性と女性に携帯を持っているかどうかを聞いてみました。そうしたら、男性は1,000人中持っていない人が100人いました。女性も持っていない人が1,000人中100人いました。この場合、男性でも女性でも持っていない人の割合は同じなので、つまり携帯を持っているか、持っていないかというのが性別によって違わない。つまり関連性がないだろうというふうに考える。これが関連性の考え方です。
さっきも出てきましたが、関連性を考えるときに、基本的には量的研究では、暗にどっちが結果で、どっちが原因だというのを仮定してというか、想定して分析をすることが多いです。結果側のほうを従属変数とか目的変数とか被説明変数というふうにいいます。これはもう頻繁に出てくるので、だいたい論文とかの方法のセクションとかでも従属変数はこれにしたとか、目的変数をこれにしたというふうに出てきます。原因側は独立変数と説明変数というふうに呼びます。これも自分で論文を書くときは、説明変数はこれとこれとこれでとかという感じで書きます。
変数の型、さっきもやりましたが、変数の種類が違えば、関連性の調べ方はもちろん違ってきます。質的変数と質的変数の関連性を見るときはクロス表を書いて、関連性を調べます。質的変数と量的変数の関連性を調べるときは、主に平均値の比較をします。量的変数と量的変数を比較するときは、共分散というものを出したりとか、相関係数というものを出して関連性を見ていきます。まとめると下の表みたいになります。
まず質的変数と質的変数の関連性を調べてみようというときに書くのがクロス表といわれる。最初に出てきた肺がんと喫煙というものです。ここは喫煙をするか、しないかということとがんを見るわけですね。呼び方としては、こっちの横方向、行と呼びますし、縦方向を列といいます。覚え方としては、それぞれの感じの右側、これが縦なので列。行はここが横にいくので行というふうに覚えると、どっちが行で、どっちが列かと覚えられるかなと思います。横方向が行で、縦が列です。
実際にはこのデータでは両方ともトータルが1,000人なので、そんなにさっきのパーセントがなくても割合は分かるんですが、実際には周辺度数、行周辺度数が同じになるとは限りません。なので、それぞれ行か列の方向にパーセントを出して、その全体の合計に依存しない値を出してあげると分かりやすい。さっきの100人と10人でも、大きさの関係は分かるんですが、パーセントに直してあげると、喫煙をしている人では10%ぐらいになる。喫煙をしない人では1%ぐらいになる。実際にはこんなに高くないと思いますが、こういうふうに表現すると、より分かりやすくなる。
通常はクロス表を書くときは度数とパーセントを両方とも示すことが多いです。列のほうにも同じようにパーセントを書くことができます。どっちに注目をするかとか、見やすさによって列方向にするか行方向にするかを決めればいい。
クロス表を書いたときに関連性の指標として使われるのが、これは疫学で使われるんですが、リスク比とオッズ比というものです。たぶん医療系のバックグラウンドのある人は、絶対、国試の公衆衛生とかそういうところで出てくると思うんですが、たぶん計算問題をやったのではないかと思うんです。リスク比とかオッズ比は幾らだとか、そういものがあったと思うんですが、こういう定義になる。
リスクというのと全体のこのうちの病気なり何なりになった人の割合。それを要因があるかないかで比を取ってあげるというのがリスク比です。オッズというのは、要因がある人、ない人の中でイベントが発生した人と発生していない人の比というのがオッズです。さらにその比を取ってあげる。要因があるかないかで比を取ってあげたものがオッズ比というものです。この場合だと、まず要因がある曝露群、要因がある人のオッズというのは、イベントが発生した人と発生していない人、つまりB分のAです。要因がない群のオッズというのは、C分の、B分Cです。なので、さらにその比を取ってあげると、オッズ比というものになります。
あとはクロス表のあれとしては、ファイ係数というのを計算することもできます。これは後で量的変数と量的変数の関連で出てくるんですが、相関係数というものの一種で-1から1の間の値を取ります。1、絶対値が多ければ多いほど関連性が強い。ゼロなら関係がないよというものです。
クロス表とかもグラフにしてあげると分かりやすかったりするので、そういったふうにグラフを書いてみるとよいと思います。
それから質的変数と量的変数の関係です。この場合は質的変数のカテゴリーごとに量的変数の平均を出してあげて比べてあげるというのが自然なアイデアだと思います。具体的にいうと、質的変数というのは性別です。ここは労働時間というのと、性別というものの関連性を見ようというときに、じゃあ、どういう割合になるかというと、労働時間に男女で違いがあるかどうかというのを見てあげればいいというアイデアになるかと思います。それで集計してみると、男性は平均の労働時間が48.8時間、1週間に。女性だと33.9時間。じゃあ、男性のほうが長く見えますねというので、これは後でまた出てくるんですが、これは本当に男女で差があるかどうか。母集団の中で差があるかどうかというのをやるときに使う検定なんですが、この段階だと、この集団の中では確かに男性のほうが労働時間が長そうだというのがこれで分かってくると思います。
箱ひげ図で書いてあげると、こんな感じです。男性と女性で中央値もそうだし、平均値もそうなんですが、労働時間の長さが違うというのが分かってくる。なので、性別と労働時間の間には何かしらの関係があるのではないかということを考えるわけです。
さらに量的変数と量的変数というものの関連性を見る。このときはどっちも量的変数というのは、とりうる値の範囲が大きいので、さっきみたいな集計をした平均と平均を出してみたりしてもよく分からない。なので、まずグラフにしてみると、より量的変数の関係、どういう関係でもそうなんですが、グラフを書いてみるというのは関連性を見るときにすごく重要なことです。今、ここに量的変数のデータ、こういう測定したデータがあります。これだけを見ても、関連があるかないかは、よほどこの数字を見てグラフを書けるような謎のコンピュータ脳を持っている人がいれば、うん、これは関連しているねというのが分かるかもしれないんですが、凡人の私とか皆さんは分からない。なので、グラフを書いてみようということになります。
このXとYをちゃんと2次元平面をプロットしてあげると、ちょっと見づらいんですが、何となく、何となくどころではないですね。右上がりになっている。つまりXが大きければ大きいほどYも大きくなるという関係があるのではないかというのがグラフから見えてくると思います。
ただ、これだけでは、いや、あんたの目がおかしいといわれてしまったら困るので、それを定量化してあげようというのが共分散だったりとか、後でちょっと出てくる相関係数ということになります。共分散も相関係数もどっちも2つの変数がどれぐらい共変動をしているかというものの程度を表しているんですが、共分散というのは、さらに先に進んで、多変量解析をするときとかにはいろいろなパラメータを計算するときの基礎になる重要な統計量ではあるんですが、関連性を見るだけであれば、こちらの相関係数のほうが分かりやすいです。
共分散というのは何で分かりづらいかというと、単位とかケース数の影響を受けるので困る。そこで出てくるのが最初の、さっき平均とか標準偏差は検査値のところで出てきた標準化という考え方です。単位とかケース数とか、そういうものの影響を受けないようにやってあげて、共分散というのを標準化してあげたものがピアソンの積率相関係数。これは大学で研究をやるといえば1回は出てくるので、これは覚えておいてください。これは量的変数と量的変数の関係の大きさを「係数」という値で表す方法です。これを-1から1の間の値を取って、0だと関係ないし、1に近いほど、「正」の関係。-1に近いほど「負」の関係があるというものです。
計算式はこんな感じで出てくるんですが、覚えていなくても勝手に皆さんがデータを分析しているときはコンピュータが計算してくれるので大丈夫です。相関係数と散布図。最初に量的変数と量的変数の関係を見るときはグラフを書いてみるといいよという話をしていましたが、散布図の形で相関係数というのが何となく分かります。完全に直線に乗っている。右上がりの直線のときは相関係数が1。逆に右下がりの直線になるときは相関係数が-。相関係数がゼロのときはこんな感じで均等にばらついているという感じになりますし、それぞれ±1に近づいていくと、この散らばり具合がギュッとなってくるというものになります。
だいたい皆さんが扱うようなデータだと、つまり質問紙のデータだと、相関係数で0.5にいくようなものはほとんどないと思います。よほどの関連があるようなものでないと、0.5クラスのものというのはあまり出てこなくて、もっと物理量だったりとか、そういうことだと工学とかそっちのほうだと、相関係数が高いような関連も出てくるんですが、社会科学系とかこういう心理系とかそういうところでは、比較的相関係数が0.5もあまり出ないものというのが結構多いと思います。
まとめると、変数の関連性を見るときも変数の型を意識をするというのは大事ですよということです。質的変数と質的変数の関連を見るときは、基本的にはクロス表というのを書けば分かります。質的変数と量的変数というものの関連性を見るときは、平均値を比較してあげれば、様子が見えてきますよ。量的変数と量的変数の関係を見るときは、相関係数を見てあげると関連性の大きさが分かってきますよということで、二変量を分析するときは、こういうものが基本になってくるということです。
統計講義動画
- 第1章 イントロダクション:データの作り方
- 第2章 記述統計と推測統計、データの型
- 第3章 1変量の集計
- 第4章 2変量の集計
- 第5章 推定と検定
- 第6章 パラメトリック検定とノンパラメトリック検定
- 第7章 パラメトリック検定
- 第8章 ノンパラメトリック検定
- 第9章 重回帰分析その1多変量解析の基礎
- 第10章 重回帰分析その2回帰分析の多変量バージョン重回帰分析
- 第11章 重回帰分析その3重回帰分析の応用
- 第12章 因子分析その1尺度による潜在変数の測定
- 第13章 因子分析その2探索的因子分析の基礎
- 第14章 因子分析その3因子の回転と解釈
- 第15章 多変量解析 ロジスティック回帰分析
- 第16章 多変量解析 構造方程式モデリング
統計コンテンツクイズ
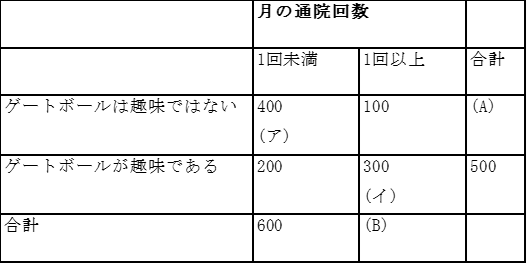
以下の表は20歳から80歳の一般住民1000名に趣味と1月あたりの通院回数を調査し、結果を集計したものである。
設問 4-1-1
表の(A)は行周辺度数である。(A)に入る数値はどれか。
行方向にセル度数を合計すればいいので、
400+100=500
設問 4-1-2
表の(B)は列周辺度数である。表の(B)に入る数値はどれか
列方向いセル度数を合計すればいいので、
100+300=400
設問 4-1-3
(ア)のセルの行パーセントはどれか。最も近いものを選べ。
(ア)のセル度数を、行周辺度数で割ってパーセンテージに変換すればいいので
400÷500×100=80%
設問 4-1-4
(イ)のセルの列パーセントはどれか。最も近いものを選べ。
(イ)のセル度数を、列周辺度数で割ってパーセンテージに変換すればいいので 300÷400×100=75%
設問 4-1-5
「ゲートボールが趣味ではない」群に対する「ゲートボールが趣味である」群の通院回数が1回以上である相対危険度はどれか。最も近いものを選べ。
趣味ではない群のリスク=100÷500=0.2
趣味である群のリスク=300÷500=0.6
趣味でない群に対する趣味である群の相対危険度は相対危険度=趣味である群のリスク÷趣味でない群のリスク =0.6/0.2=3
設問 4-1-6
「ゲートボールが趣味でない」群に対する「ゲートボールが趣味である」群の通院回数が1回以上であるオッズ比はどれか。最も近いものを選べ。
趣味ではない群の通院1回以上オッズ=100/400=0.25
趣味である群の通院1回以上オッズ=300/200=1.5
趣味でない群に対する趣味である群のオッズ比は
オッズ比=趣味である群のオッズ÷趣味でない群のオッズ
=1.5/0.25=6
設問 4-1-7
これまでの分析結果から導かれる結論として妥当なものはどれか。
関連性があることはわかるが、これだけでは因果関係があるとはいえない。因果関係と相関関係の違いに注意しよう。
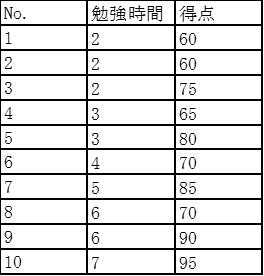
以下の表はある高校の生徒の勉強時間と試験の得点をまとめたものである
設問 4-2-1
勉強時間が3時間以下の群と4時間以上の群の平均得点の組合わせはどれか。
・3時間以下の群(A群)
(60+60+75+65+80)/5=68
・4時間以上の群(B群)
(70+85+70+90+95)/5=82
設問 4-2-2
データをもとに計算したところ、勉強時間が3時間以下の群の得点の標準偏差は8、4時間以上の群の得点の標準偏差は10であった。このとき、2群間のテストの点数の差の大きさの指標であるCohen’s dの絶対値はどれか。
Cohen’dは以下の式で計算できる。
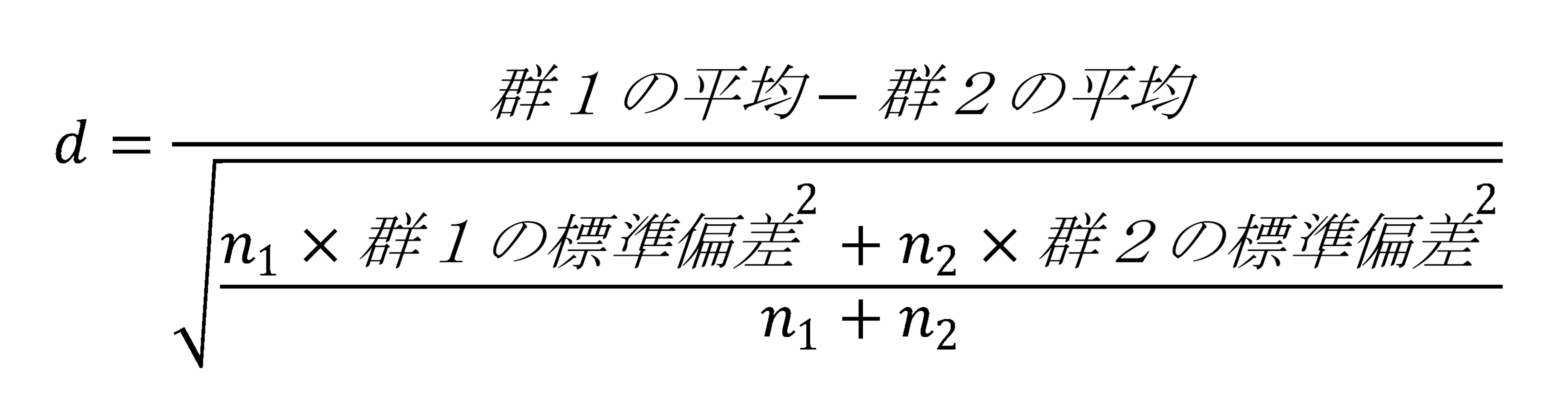
n1: 群1の人数,n2: 群2の人数
群1を勉強時間4時間以上、群2を勉強時間3時間以下とすると、
群1(4時間以上群)の平均=82、標準偏差=10、群2の平均=68、標準偏差=8なので
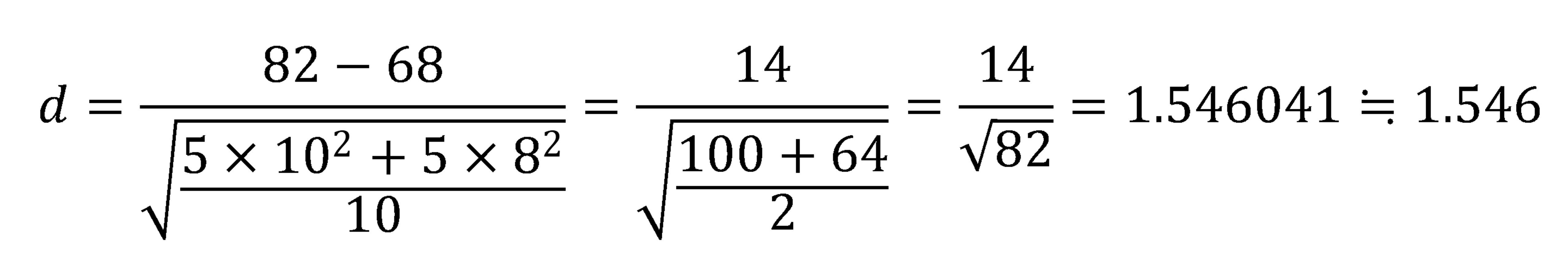
下の表はある高校の生徒の勉強時間と試験の得点をまとめたものである。
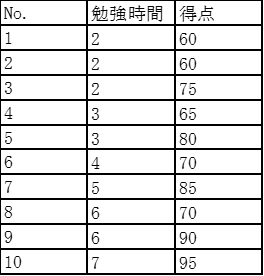
設問 4-3-1
勉強時間と得点の共分散はどれか
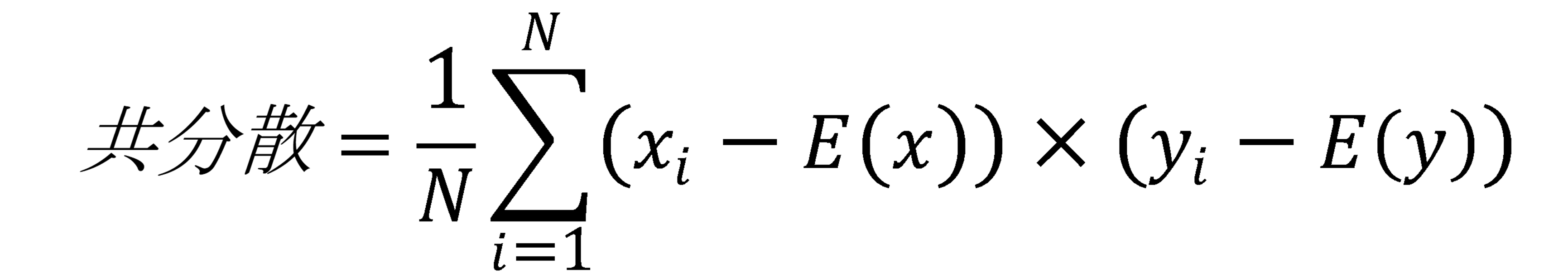
各ケースの各変数の偏差の積の和をケース数で割る(偏差の積の期待値)
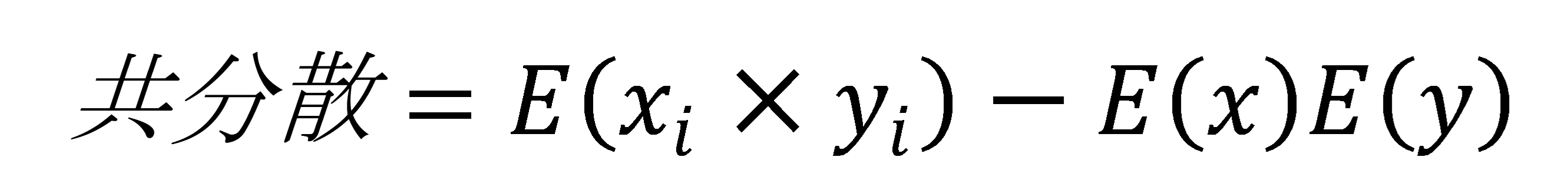
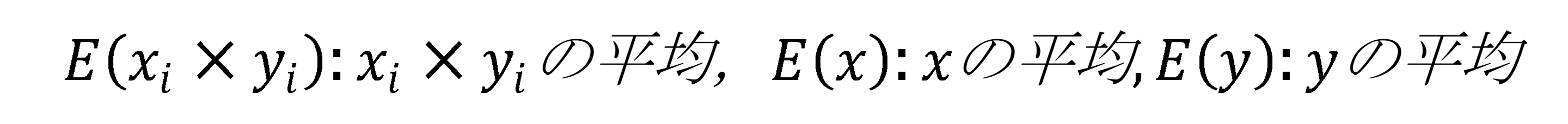
各ケースの変数の値の積の平均から各変数の平均の積を引く
共分散=((-2)×(-15))+((-2)×(-15))+…+(2×15)+(3×20)/10=155/10=15.5
設問 4-3-2
勉強時間と得点のピアソンの積率相関係数はどれか。なお、勉強時間の標準偏差は2、得点の標準偏差は12とする。
ピアソンの積率相関係数は以下の式で計算できる
・XとYの共分散を、Xの標準偏差×Yの標準偏差で割って標準化する
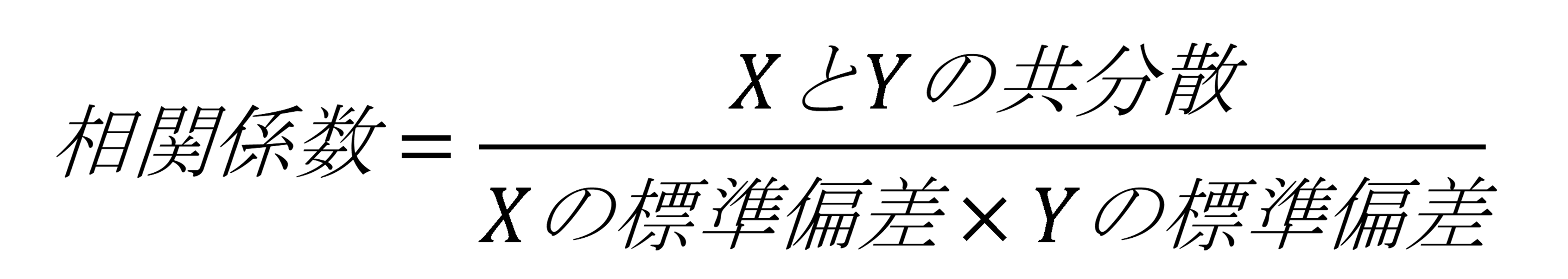
勉強時間と得点の共分散は15.5だから
相関係数=15.5÷(2×12)=15.5÷24=0.6458≒0.65
設問 4-3-3
勉強時間と得点の関係はどのような関係にあるか。
ピアソンの積率相関係数(相関係数)はマイナス1から1の値をとるもので、0だと線形関係にはない、1に近いほど、「正」の線形関係がある、マイナス1に近いほど、「負」の線形関係があることがわかります。
大まかな相関の強さの目安(分野によって異なるので注意)は以下の通りです。
相関係数の絶対値が
0.1未満: 無視できる、0.1~0.3: 弱い相関、
0.3~0.5: 中程度の相関、0.5以上: 強い相関
2)で相関係数は0.65だったので、勉強時間と得点は「正の相関関係にある」というのが妥当です。