第10章:重回帰分析その2回帰分析の多変量バージョン重回帰分析
ナレーション原稿
(スライド番号22から)
米倉 じゃあ、こういったいろんな複雑な変数が、第3の変数を考慮してしようとすると、複雑になってくるというのを、どのようにしてですね、統計の集めたデータを使って表現をして、その関連の複雑な状態というのを表現するかというところをですね、これから見ていこうと思います。
そのようなですね、多くの変数の関係を記述する統計モデルの一番初歩的な、基本的なモデルが、この重回帰分析というものです。この回帰分析というところを見てピンとくる人が多いんじゃないかと思いますけども、この前やったですね、この回帰分析を少し拡張したのが重回帰分析。ちょっと復習ですけども、回帰分析というのは、量的変数同士の関係を直線関係にモデル化したもので、このように一次関数で目的変数と説明変数の関連というのを表現しています。これも復習ですけども、このXですね。原因側にくる変数のことを独立変数、説明変数、曝露というふうに言って、結果側に来る変数のことをですね、目的変数、従属変数、応答変数、被説明変数というふうに呼んでいました。この回帰分析ではですね、集めてきたデータを使って、この傾きと接点の値を求めるということをしていました。この傾きのことを、回帰係数ですね。ここの回帰分析の文脈では、傾きのことを回帰係数というふうに呼んでいたということですね。回帰係数には2種類あって、単回帰分析のときはそんなに気にしなくてもよかったんですけども、多変量解析のときには、よりこの標準化したか、していないかというものの違いというのが出てきます。
非標準化偏回帰係数というのは、これも復習ですけども、その変数が1単位変化したときに変数が何単位変化するかというのを表しています。式に含まれる変数の単位が変わると値が変わってしまうので、単位に注意をしないといけない。値が大きかったといっても関連が強いとは限らないというのが、非標準化偏回帰係数というものです。この非標準化偏回帰係数のほうは、変数の値そのものに意味がある場合には使いやすいので、比尺度ですね。比尺度である長さとか、おそらくは金額とかですね、そういうようなものを回帰分析で使うときには、非標準化偏回帰係数のほうが理解しやすい。結果を解析しやすいという特徴がありました。
一方でですね、標準化した偏回帰係数ですね。標準化偏回帰係数というのは、目的変数と説明変数のうち、量的変数を平均0、分散1に標準化したデータを使って推定した偏回帰係数というのが、標準化偏回帰係数というものになります。標準化偏回帰係数の値というのは、説明変数が1標準偏差変化したときに、目的変数が何標準偏差変化するかというのを表しています。単回帰分析の場合は、ピアソンの積率相関係数と一致するのが、この標準化偏回帰係数というものになります。標準化偏回帰係数の特徴としては、式に含まれる変数の単位に依存しないので、複数の説明変数があるときに比較をする、大きさをですね、比較して、関連の強さを比較することもできるというのが標準化偏回帰係数の特徴というものでした。
これも復習ですけども、回帰分析の切片からわかることということですが、回帰分析の切片というのは、回帰式で説明変数に0(ゼロ)を代入したときの目的変数の値というのが、回帰式の切片の意味です。このあとやっていく重回帰分析で言えばですね、説明変数すべてに0を代入したときに、目的変数の平均がいくつかというのを表しているのが切片というものになります。なので、説明変数の値が0にならないような変数の場合には、意味がないということもあるわけですね。あとは理論上説明変数の値が0を取り得る場合でも、分析対象に説明変数の値が0となるような対象が含まれない場合には、意味のない値が出るということもあるということで、これも前に、回帰分析で出てきましたけども、年収のデータを22歳から65歳から得たとして、回帰分析で分析をして出てきた切片というのは、このままだと解釈としては0歳の平均年収ということになってしまうわけですけども、実際にはこの範囲以外にこの回帰式の解釈というかですね、値を外挿して、拡張して解釈するというのは、できないことが多いので、これはあくまでも22歳から65歳のあいだでだけ通用する式だということですね。なので、場合によってはですね、この切片の値がきちんと解釈できるような値になるように、説明変数の値を変換して、平均値がちょうど0になるように説明変数を変換したあとで分析をしたりすることもあります。こういう操作のことをですね、説明変数から平均を引く操作のことを中心化というふうに言ったりすることもあります。
それから、回帰係数の意味ですね、回帰係数からわかることですけれども、回帰係数の値というのは、説明変数の値が1大きくなると、目的変数の値がいくつ大きくなるか、もしくは小さくなるかというのを表しています。回帰係数の値が0より大きい場合には、説明変数の値が大きくなると、目的変数の値も大きくなるということを意味していて、言い換えると、2つの変数が正の相関関係にあるということわかります。一方で回帰係数の値が0より小さい場合、マイナスの値のときは、説明変数の値が大きくなると、目的変数の値が小さくなるということがわかります。言い方を変えると、2つの変数が負の相関か関係にあるということが、回帰係数の値がマイナスのときにわかるということですね。非標準化回帰係数は、目的変数と説明変数の単位によって値が変わるので、説明変数の単位によっては、データを1つ上げたり、下げたりすると、10倍になったり、10分の1になったりするわけですね。さっきの年収のデータで言うと、年収の単位を千円にすると、切片はもともとが240万円だったので、この値としては2,400千円、回帰係数は0.5万円だったのが、これは0.5万円なわけですけども、年収の単位を千円にすると、5千円に変わるので、このような式になると。なので、実際に関連の強さは変わらなくても、この単位を変えると、この回帰係数の値というのが変わるので、目的変数と回帰分析の結果を見るときには、目的変数と説明変数の単位に注意をする必要があります。非標準化偏回帰係数が使われている場合には、単位に注意する必要があるということになります。
あとは、この回帰分析をですね、視覚的に表現したものが回帰直線ですけども、この回帰分析というのは、このそれぞれのデータ点がこのように散布図で示すと、この散布図の点のちょうど真ん中辺りに通るように、線の傾きと切片を決めてあげるということをしています。当然ですね、フリーハンドでですね、適当に引いているわけではなくて、何か数量的な基準を設けて、この線の傾きと切片というのを決めているわけです。その数量的な基準がこの最少二乗法というもので、この回帰直線とそれぞれの点までの、回帰直線の予測される値と、それぞれの点の実際の値との差を取って二乗したもの。残差平方と言います。この回帰式で予測した値と、実際のことを値ですね。データとして得られた値の差のことを残差と言って、残差の二乗のことを残差平方と言います。さらに残差の、残差平方をすべてのデータについて合計したもののことを残差平方和と言って、英語ではsum of squaresというふうに言います。これが最も小さくなるように、切片と傾きを決めてあげるということをしていたのが回帰分析ですね。単回帰分析でした。
ちょっと復習をしましたけども、回帰分析というのはこういうもので、さらに重回帰分析というのは、この単回帰分析を拡張して、説明変数を複数にしたもののことを重回帰分析というふうに言います。重回帰分析の場合は、説明変数が複数になるので、このようにですね、さっきはではXが1つだけだったんですけども、Xがn個とですね、理論上はサンプルサイズ、説明変数が含めることができる上限の数はサンプルサイズまでなんですけど、実際にはそこまで入れると意味がない回帰式になってしまうので、ある程度説明変数は、意味があるもの、判明しそうなものというのを選択して、使う必要があるということですね。重回帰分析はですね、回帰分析を拡張したものなので、この誤差に回帰分析の仮定を置いていましたけども、誤差の分布の仮定は単回帰分析と同じで、独立に、個々の残差は独立していて、さらに正規分布に従っていると。あとはどの区間でもばらつきは同じだという、独立性、正規性、等分散性という3つの仮定を置いています。誤差に。重回帰分析で、大きく回帰分析と変わるのは、この偏回帰係数の解釈です。あとは、そのあと偏回帰係数というふうに、さっきまでも言っていましたけども、偏回多変量ですね、重回帰分析になると、単なる回帰係数ではなくて、偏回帰係数ですね。英語だとpartialですけど、partial regression coefficientと言ったりしますけども、この偏回帰係数という呼び方に変わります。この偏回帰係数の解釈が、単回帰係数とは違っていると。どういう解釈になるかというと、注目する変数以外の変数の値を固定して、注目する変数だけを変化させたときに、目的変数とどのような関係にあるのかということをですね、偏回帰係数は表しています。つまり偏回帰係数というのは、ほかの変数の影響を取り除いた、その変数独自の関連性ですね。今。影響力と書いてありますけど、影響力、関連性、目的変数との関連というのは、ほかの変数の影響を取り除いたものであるということですね。なので、交絡要因ですね、交絡とかの統制に使われるわけですね。少しイメージで書くと、この目的変数との重なる部分というのが、関連性の強さだというふうに考えてもらえればいいんですが、この重回帰分析ではですね、ほかの説明変数と重なり合う、こういう独自ではない部分というのは除去されて、この独自に目的変数と重なっている、関連するところだけが偏回帰係数として出てくるような計算をしています。詳しい計算のしかたは、この授業ではやりませんけれども、偏微分とかを使ってですね、1つの変数だけを動かしたら、この係数はいくつになるかというようなことをですね、求めてということになります。これが重回帰分析の考え方なんですね。この説明変数独自の関連性ですね。説明変数独自の目的変数との関連性というのを求めるために使っているのが、この重回帰分析のほうになります。
それから、これは重回帰分析ではなくても実はできたんですけども、回帰分析の説明変数に、質的変数を使うということもですね、ここで導入をしておきたいと思います。回帰分析は通常、量的変数同士の関連を見るときに今までは使うというような話をしてきました。ただ、実際にですね、多くの統計ソフトで回帰分析のメニューからやると、説明変数も、目的変数も、両方とも量的変数として扱われるんですね。なので、名義変数を数値データに置き換えて、回帰分析の説明変数にすると、解釈することができないということですね。なので、回帰モデルでどうにかしてですね、この質的変数と量的変数の関連を見たいというときには、工夫が必要になってくるというわけです。例えば、この名義変数の例として、都道府県に北から順番に番号を振って、北海道なら1、青森なら2、岩手なら3、沖縄は47というふうに振ったとしましょう。そうすると、県番号と、あとはここ、連続量、量的変数として一人あたり所得というのがあります。これを散布図に描くとこういうふうになっていて、なんとなく二次関数のように見えますけども、実際にこんなに一般化できると言ったらあれなんですけども、わけではなくて、これを直線で表現しようとすると、これをそのまま、つまり県番号を量的変数として扱って、両方とも、一人あたり所得と県番号の両方を量的変数として扱って回帰分析をすると、こういう式が出てきます。一人あたり所得というのは、3014.9-8.81×県番号。つまり、県番号が大きくなればなるほど、一人あたり所得が少なくなっていく。ただ、なんかおかしいなというような感じが皆さんしているんじゃないかと思うんですけども、実際におかしくて、こういうような表現のしかたよりは、どこか基準となる都道府県というのを決めてあげて、その都道府県のあいだの、平均の差として解釈できたほうが、つまり、それぞれの、一個一個の所得のあいだの差としてですね、出てきてくれたほうがいいじゃないかと。実際に今まで平均の、質的変数と量的変数の関連を見るときには、平均を比較していたじゃないかというふうに考えることができるわけですね。つまり、回帰分析で、じゃあこのグループとグループのあいだの平均の差というのを、どうやって表現するかということを考えたほうがよさそうというのが、質的変数を説明変数として使うときには考える必要があると。この都道府県の例で言うと、都道府県のこの県番号を量的変数として扱うのではなくて、質的データとして扱って、北海道と青森の平均の差はいくらとか、北海道と岩手の差はいくらというようなかたちで、平均を比較できるようなモデルにできないかということを考えるんですね。この平均の差を比較できるようなモデルをつくるために使われる工夫というのが、ダミー変数というものです。このダミー変数を使うことで、この回帰係数を平均の差として解釈することができるようになります。どんな考え方をしているかというと、ダミー変数というのは、質的変数のカテゴリというのを、グループを0と1の組み合わせで表現をするわけですね。さっきの都道府県とは違いますけども、男女とかですね、学歴とか、大卒、専門・短大卒、高卒、中卒というふうにあると。このグループ間で比較をするときに、この回帰係数ですね、偏回帰係数の値がそれぞれのグループのあいだの差だというふうに解釈できるようにしてあげるというのがこのダミー変数で、この0、1で表現をしてあげることで、このダミー変数の偏回帰係数の値というのが、参照カテゴリと該当するカテゴリの平均の差として解釈することができる。参照カテゴリというのはいったい何かというと、ダミー変数の値がすべて0のカテゴリです。こっちの性別で言うと、男性が参照カテゴリで、女性、このダミー変数を使ってですね、回帰分析をしたとすると、回帰係数の値は、男性に比べて女性がどれぐらい高いか、低いかというのを表すものになると。こっちの学歴のほうで言うと、中卒の人はみんな、この3つのダミー変数の値が0になって、中卒と比べて、このD3の回帰係数は、高卒の人、高卒の人は中卒と比べてどれぐらい高いか、低いかというような、平均の差としてですね、この回帰係数というのは出てきます。このダミー変数を使うことでですね、質的変数というのを回帰分析のなかに組み込んで、平均の差として偏回帰係数で解釈することができるようになるということですね。実際の例として、これは食に関する視覚的QOLというのがあって、食生活の充実度のようなものというふうに考えてもらえばいいんですけども、この同居状況というのがダミー変数として質的変数、それから同居者がいるか、いないかというのをダミー変数にしています。値が0ですね。同居状況の変数の値が0だったら同居。同居者がいる。1だったら単身ということで、ここに出てきているこの係数、-2.192というのは、同居者がいる人に比べて、単身の人では、この食に関する主観的なQOL、主観的QOLというものの得点が2点低い。-2.192だけ高いので、つまり、2.192点低いということですね。このようなかたちで、ダミー変数を使うことで、2グループの比較というのを回帰係数に組み込むことができて、その2グループの組み合わせを考えることで、複数、3グループ以上の比較というのも、この参照カテゴリとの比較というかたちで表現することができるというのが、このダミー変数を使った回帰分析というものになります。
あと重回帰分析になって、この非標準化偏回帰係数と標準化偏回帰係数の解釈がどうなるかというところなんですけども、基本的に両方とも解釈のしかたというのは、単回帰分析の回帰係数の解釈とほぼ同じです。違いは、ほかの説明変数の値を0の固定をしたという条件が加わるだけで、説明変数と目的変数の関連を表しているという点は同じですね。ほかの説明変数の値が0だったとしたら、説明変数と目的変数はどんな関連があるかというのを見てみます。見てみるというか、出してくれるのが重回帰分析の非標準化偏回帰係数の解釈ということになります。それから、あとは、同じような解釈ができて、説明変数が量的変数なら傾きを表していますし、質的変数なら参照カテゴリとの平均の差を表しているのがこの非標準化偏回帰係数になります。標準化偏回帰係数も、解釈のしかたは同じで、ほかの説明変数値を0に固定をしたときの説明変数と目的変数の関連ということになります。あとは、変数と関連性の強さを比較したいときは、量的変数と質的変数で直接回帰係数の値を比較するというのが、値の意味が、量的変数同士の関連で、標準化偏回帰係数の場合は相関係数のようなものとして解釈できるんですけども、質的変数が説明変数の場合は、相関係数のようなものとしてですね、解釈することができない。ここに書いてあるとおり、1の意味がですね、説明変数が量的変数の場合は、1標準偏差、説明変数が1標準偏差で動いたときに、目的変数が何標準偏差で変化するのかというのを表しているのに対して、説明変数が質的変数の場合は、参照カテゴリに比べて、目的変数の値が何標準偏差違うかというのを表しているので、この説明変数の1の意味が違うので、直接比較することができます。なので、関連の強さを比較するときは、相関比と言って、イメージとしては分散分析のときにやった、このそれぞれのグループだったりとか、変数で説明することができる、目的変数のばらつきを比較することで、関連性の強さというのを評価するということをします。その指標が相関比というもので、これは全体の平方和、モデル全体の平方和というのを分母にして、それぞれの変数で説明できる平方和を割ってあげたものというのが、この相関比というものになります。これを比較することでですね、関連の強さというのを比較するということができると。この場合だと、性別とコントロール感という変数が、あとは疾患の有無とかというのもあるんですけども、これの相関比を計算すると、ここのタイプⅢ平方和というやつを、この総和というやつで割ってあげて計算しています。これは皆さん、今の段階では計算できる必要はなくて、こういうのがあるというのを知ってくれていればいいんですけども、ただの割り算なので、計算はそんなに難しくないと思いますが、このように計算して、性別とコントロール感を比較すると、コントロール感のこの相関比のほうが大きいので、コントロール感のほうがこの目的変数であるCES-Dですね、精神健康度との関連は強いというのがここからわかるということですね。
あと重回帰分析を論文で結果を示すときは、このような表にまとめて出すことが多いです。説明変数ですね。説明変数をこっちの1列目に配置して、それぞれに説明変数に対応する偏回帰係数の値と、あとは検定の結果というのを示すのがスタンダードな結果表記のしかたになるかなと思います。あとは、この表だと、このβというふうに偏回帰係数の表記が書かれているんですけど、このβというふうに書くと、少なくとも看護系であればですね、このβというのは標準化偏回帰係数を表しています。ただ分野によってですね、この書き方、表記のしかたというのは、ルールというかですね、違ったりするので、より丁寧にするのであれば、このように略すのであれば、この表の注釈のほうに、このβはいったい何を表しているのかというのを書いたほうがより丁寧なですね。いずれにしても、看護系の論文であれば、βと書いてあったら標準化偏回帰係数だと思えばいいです。あとは、この偏回帰係数の検定結果というのが載っていて、有意だったらどういう解釈ができるかというと、通常はですね、この回帰係数の検定というのは、回帰係数の値が0かどうかというものの検定をしています。つまり、帰無仮説が偏回帰係数=0ということですね。なので、この帰無仮説が棄却されるということはどういうことかというと、偏回帰係数は0とはいえないということなので、つまり偏回帰係数が0ではないということは、関連があるということなので、検定で有意であれば、有意な関連があるというふうな表記というかですね、文章としてはそのように書かれます。
それから、これはこのあと出てきますけども、この重回帰分析で何か予測をしたいというときにはですね、このように、決定係数というのを示したり、モデル間でですね、あてはまりのよさというのを比較したりというときには、こういう決定係数を出して、あてはまりを比較したりするというようなこともあります。
それから重回帰分析ですね、回帰モデルで重回帰分析などで、最初のほうにやったですね、交絡とか、媒介とか、抑制とか、歪曲とか、修飾とかというのは、どうやって表現をするかと。表現して確認するかというところもちょっと見ておこうと思います。
交絡と媒介というのは、どうやって確認をするかというと、注目する要因だけを投入するモデルと、注目する要因に加えて、交絡要因の候補ですね、もしくは媒介を見たときは媒介要因の候補を同時に投入するモデルを比較するということをします。このモデルをですね、比べる。モデルを比べて、出てくる偏回帰係数の値を比べるということを、交絡、媒介、抑制、歪曲の確認をするときにおこないます。交絡や媒介であればですね、注目する要因だけを投入する、投入した分析の結果と、この交絡要因を同時に投入した分析結果を比べて、最初に注目する要因だけ投入すると目的変数と関連があって、交絡要因をさらに追加すると、関連が消えてしまうと。注目する要因と目的変数の関連が消えてしまうと。そういうときにはですね、交絡、もしくは媒介が起こっているというふうに考える。あとは注意が必要なのは、交絡が起こっているのか、媒介が起こっているのかというのは、関連性の分析結果だけではわからないので、理論的な考察、つまりそのメカニズムについてですね、先行する研究だったりとか、理論をもとに考察する必要があると。関連性の分析だけではどっちかというのは決定できないということがあります。それから、抑制とか歪曲についてですね、これも交絡、媒介と考え方は同じで、注目する要因だけ使った分析結果と、注目する要因と、あとは抑制変数、もしくは歪曲変数の候補となる変数を同時に含めた重回帰分析の結果というのを比較して、最初の注目する要因だけ投入すると関連がない。抑制変数を同時に投入すると関連が出現する。もしくは関連性の符合が逆になったらですね、歪曲が起こった可能性があるというふうに考えると。いずれにしても、注目する要因だけを含めた分析というのと、注目する要因に第3の変数ですね、交絡とか、媒介とか、抑制とか、歪曲を引き起こしそうな変数を入れた場合、比べてみて、結果がどういうふうに変わるかというのを見ることで、これらの現象が起こっているかどうかというのを確認することができるということですね。
あとは修飾ですね。修飾だけは、ちょっと見方が特別というか、違っていて、修飾が起こっているかどうかというのを見るときには、交互作用項というものをですね、追加して、関連があるかどうかを見ることで確認することができます。交互作用項というのは何かというと、注目する要因と、効果を修飾すると考えられる要因の、変数の値の積、つまりかけ算をしたものを投入するというのが、修飾が起こっているかどうかを見るときの分析方法です。なんで、これで修飾が起こっているかどうかというのを、修飾を表現できるかというと、モデルの式を書いてみるとわかりやすいかなと思います。交互作用を入れたですね、含めた回帰モデルというのは、こういう式になると。説明変数𝑋1と𝑋2があって、これが交互作用ですね。𝑋1と𝑋2のかけ算。これを、例えばですね、𝑋2が修飾、𝑋1とこのYの関係というのを修飾する要因だというふうに見て、𝑋1についてこの式をですね、この右辺を整理してあげると、このように変形することができます。切片足すもともとの傾き、プラス、この𝑏3ですね。交互作用項の偏回帰係数かける𝑋2の値。この2つの要素によって、この𝑋1とYの関係というのが変わると。つまり、𝑋2の値によって、この𝑋1とYの関連性というのは変わるというのをこの部分で表現することができているわけですね。なので、こういう分析をすることで、この修飾が起こっているかどうかというのを見ることができて、この交互作用の偏回帰係数というのは、修飾の効果の大きさというのを表しているということになります。この交互作用のですね、偏回帰係数が0に近ければ修飾は起こっていないというふうに見ることができますね。この𝑏3の値が0に近くて、有意でもないようなときには、この交互作用というのはなくて、つまり効果な修飾というのは起こっていないというふうに解釈することができるということになります。
統計講義動画
- 第1章 イントロダクション:データの作り方
- 第2章 記述統計と推測統計、データの型
- 第3章 1変量の集計
- 第4章 2変量の集計
- 第5章 推定と検定
- 第6章 パラメトリック検定とノンパラメトリック検定
- 第7章 パラメトリック検定
- 第8章 ノンパラメトリック検定
- 第9章 重回帰分析その1多変量解析の基礎
- 第10章 重回帰分析その2回帰分析の多変量バージョン重回帰分析
- 第11章 重回帰分析その3重回帰分析の応用
- 第12章 因子分析その1尺度による潜在変数の測定
- 第13章 因子分析その2探索的因子分析の基礎
- 第14章 因子分析その3因子の回転と解釈
- 第15章 多変量解析 ロジスティック回帰分析
- 第16章 多変量解析 構造方程式モデリング
統計コンテンツクイズ
慢性疾患患者の生活の質に関連する要因を検討するため、質問紙調査を行った。
調査した項目は表の通りであった。

設問 10-1-1
調査した項目のデータを分析して、生活の質に独自に関連する要因を見つけたい。適切な分析方法はどれか。
重回帰分析以外の分析は2変量の分析なので、独自に関連する要因を見つけるには適当ではない
→重回帰分析が正解
設問 10-1-2
調査した項目のうち、分析する際にダミー変数を作る必要がない変数はどれか。
ダミー変数を作る必要がないのは、量的変数
上記のうち量的変数は「年齢」だけなので「年齢」が正解
設問 10-1-3
疾患の種類を分析の説明変数として使うためダミー変数を作りたい。ダミー変数は最低何個作る必要があるか。
質的変数のカテゴリを表現するには最低(カテゴリ数ー1)個のダミー変数が必要
「疾患の種類」は4カテゴリあるから4ー1=3個のダミー変数が必要になる
設問 10-1-4
分析を行い、表のような結果が得られた。この結果から言えることはどれか。全て選べ。ただし、有意水準は5%とする。
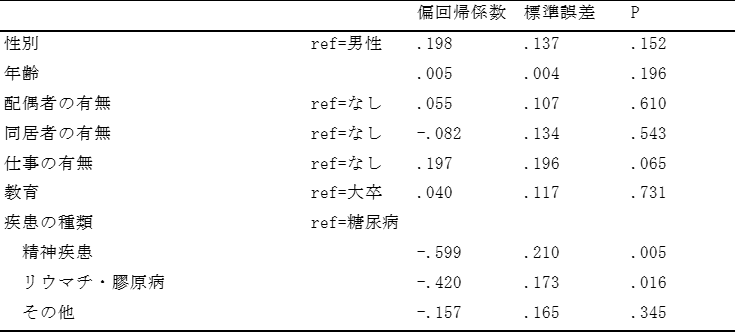
a. 男性より女性の方が生活の質が低いが、有意な関連ではない。
→誤り: 男性が参照カテゴリで偏回帰係数は0.198なので女性の方がQOL得点が高い。P値は0.152なので有意ではない。有意な関連ではないのはあっているが、女性の方が低いというのは誤り
b. 年齢が高い方が生活の質が高いが、有意な関連ではない。
→正しい。年齢の偏回帰係数は0.005で、年齢が1歳高いと生活の質の得点は0.005点高く年齢が高いと生活の質が高いと言える。しかしP値は0.196と有意水準の5%よりも大きいので有意な関連ではないと言える
c. リウマチ・膠原病の患者は糖尿病患者と比べて有意に生活の質が低い。
→正しい。「リウマチ・膠原病」の偏回帰係数は-0.420であり、参照カテゴリの「糖尿病」をもつ人よりも生活の質が0.420点低いことがわかる。さらにP値は0.016と有意水準の5%よりも小さいため有意な関連であることがわかる
d. 仕事がある人の方が生活の質が有意に高い。
→誤り: 仕事の有無の偏回帰係数は0.197で「なし」の人より「あり」の人の方が高いのはあっているが、P値が0.065で5%水準では有意ではない