第3章:1変量の集計
ナレーション原稿
この尺度によって集計の仕方が違ってくるので、ここからは、じゃあ、こういうデータをどうやって集計していくかという話になっていきます。
質的データと度数分布表。ちょっと難しい言葉のように見えますが、単純にそれぞれの選択肢がどれぐらい選択されたかとか、そういうのを示したりとか、あとは割合とか比率、相対度数というものを表記したこういうもの、これが度数分布表というものの代表例です。
これは原因物質別の食中毒の発生件数をまとめたものですが、実際、これは調査票を使って集計しているわけではなくて、食中毒統計というもので調査票を使っているといえば使っていますが、原因物質、細菌が原因だった食中毒というのは、発生検査が580件あって、全体の中で46.3%を占めていますよという件数とそれが全体に占める割合を主に示すのが度数分布表というものです。原因物質というのは質的変数です。細菌とかウイルス、化学物質、自然毒、その他不明というのは単に分類するためだけのものということで、細菌が1、2、3、4、5、6と振られていたとしても、ウイルスが細菌の倍、やばいとか、化学物質が3に振られていると細菌の3倍ぐらい致死率が高いとか、そういうことを示しているわけではなくて、単に分類しているだけというものを集計するときは度数分布というものを出します。
あと、数字だけを見ても、パッと見よく分からないということがあるので、こういうのをグラフにして視覚的にこのデータを表現することもあります。
いろいろな示し方があります。棒グラフにしたりとか、帯グラフにしたりとあります。円グラフとかも使われたりするんですが、円グラフはあまり使うなといわれています。なぜかというと、幅が解釈しにくいというか、いっぱいこういうカテゴリーが出てくると、割合というのが円の中なので結構判別しにくいというのがあるので、一番よく使われるのが棒グラフ。これだと直感的にどれが多い、どれが少ないというのが分かるというか多さを示すときでは分かるので、こういうものが好まれると思います。
それから量的変数と間隔尺度で取るものだったり、比尺度で取っていくもの。この場合は身長です。学校保健統計の身長のデータを集計したものですが、身長というのは比尺度ですね。ゼロだったら身長の長さがないというあれなので比尺度です。比尺度だと基本的には質的変数ができることは量的変数でもできます。逆は無理ですが。なので、量的変数である身長を出そうと思えば度数分布が出せる。ただ、量的変数の場合は、こういうそれぞれの値が質的変数に比べて膨大であることが多いです。身長は今センチ単位で区切っていますが、0.1cm単位とかにしたら、さらに10倍値が増えてきますし、基本的にはこういう連続的な量というのは、ほぼ無限に階級があるので、これだけのものを表にまとめようとすると、表が膨大になってしまいます。なので、値を適当な幅で区切って集計してあげるということをすることが多いです。例えば身長であれば10cm区切りで区切ったりとか、5cm単位で区切ったりとか、いろいろあるんですが、こういう形で度数分布を示したりするともあります。
あとは後で出てきますが、単純には量的変数であれば代表値、平均値、ばらつきの指標、標準偏差、そういうのを計算して集団の特徴を示すこともできるんですが、度数分布であえて示すとしたら、こういう形で度数、階級を区切ってやってあげると見やすくなりますよということです。
こういうのをさっきの棒グラフのようにすると、ヒストグラムというふうに呼ばれてそれぞれの値に対応してどれぐらいその値に当てはまる人がいるかというのを表すことができます。
ほかにも量的変数の分布の特徴、記述統計、分布の特徴を記述するために出せるというのがあります。それは平均値です。これはよく見ると思います。年齢であれば、平均年齢とか身長も平均的な身長を出していきます。平均値はたぶん皆さん、知っていると思うんですが、全てのデータを足し合わせて、足し合わせた人数とか度数で割ることで出てくるのが平均値というものです。
これは外れ値というものの影響を受けます。外れ値はどういうものか。よく例に出されるのが世帯年収とか貯蓄額とかそういうものが出てきます。きのう何かでちょっと見たんですが、貯蓄額というのが、日本人の平均だと1,700万ぐらいだというふうにいわれた。ただ、そんなに貯蓄をしている人はどれだけいるのかというと、一般庶民でももうちょっと60代とかそのぐらいになって、退職金でももらったら、それぐらいはいくかもしれないですが、私ぐらいの世代だと、そんなにないよ、平均的にいってもないよ。
なぜそういうことが起きるかというと、ソフトバンクの孫さんが数百億を持っていたりとか、そういう人たちが思いっ切りつり上げて平均が上がる。それが外れ値というものです。そういった外れ値の影響を受けるというのが平均値というものです。
できるだけ外れ値の影響を受けないような代表値を使いたいなというときに出てくるのが中央値というものです。これは全てのデータを小さい順に並べたときにど真ん中に来る値のことです。データ数が偶数のときは、真ん中の値がこっちにならないので、真ん中の2つとちょうど真ん中のものから2番目のケースと1番目のケースのものを足して2で割ったものが中央値となります。ゆがんだ分布で年収とかそういうものみたいにゆがんでいた分布だったりとか、あとは外れ値が多いような分布、そういうのでは中央値を使って代表値とすることが多いです。
あとは順序尺度も1の値は意味がないです。つまり足し算をしても意味がないということは、平均値を出しても意味がないというふうにいわれるので、順序尺度を用いる場合は代表値は中央値を使ったほうがいいよという人もいます。それから最頻値というのは、これは名義尺度で使えるんですが、データの出現が最大の値というものです。というのを代表値として出すこともあります。さっきの度数分布表でいえば、細菌というのが最頻値ということになっています。
実際の数値の例を出してみると、商品の値段がこういうデータがあって、これを全部足し合わせて割ってあげたのが平均。中央値というのは、これを小さい順に、大小と並べてちょうど真ん中に来るものが中央値。最頻値というのは、度数分布を出してみて、一番度数が多い、これが最頻値ということになります。
グラフで見て意味があるのかというあれもありますが、こんな感じで視覚的にまとめることができます。
あとは量的変数の特徴としては代表値のほかに、ばらつきというものがあると、より集団の様子を捉えることができます。同じ平均値でもこれは全部、ここに出ているグラフ、全部、平均値が同じ。平均が10の正規分布というものですが、ばらつき、標準偏差から1のときと5のときと10のときで分布の様子がだいぶ違います。標準偏差が大きいほうがばらつきが大きいので、ばらつきが大きいとこういうふうに山が低くなって、裾野が広くなる。こういう分布になったりとか、標準偏差、ばらつきが小さいときに分布が集中してくるとか、こういう特徴を示すときに、ばらつきというものが使われます。
量的研究だとばらつきというか、平均とかそういうのを出して平均がどれぐらいだというのをいっているのではないかという人も多いです。実際には統計、量的研究というのはばらつきのほうに注目するものです。なぜ、ばらつくのかというのをやるのが統計解析だし、量的研究ということです。もちろん平均を出すのも重要な役割ではあるんですが、基本的には量的研究で注目するのはばらつきです。なぜばらつくのかということをやります。
ばらつきの指標、いろいろなものがあるんですが、これはそんなにメジャーではないというか、あまり使われないというものではあるんですが、ご紹介だけをしておきます。範囲というものです。最大と最小というのを引いてあげたりとか分位数、ここら辺はちょこっと出てかもしれません。変数を値の順番に並べた上でさっきの中央値と同じ考え方です。等しいサイズに分割する値。例えば4分の1、25%ずつ区切る。あるいは4分位と呼ばれたりとか、5分の1、20%ずつで区切るときは5分位と呼ばれたりします。第3四分位数と第1四分位数、つまり75%にあたる人と、25%にあたる値の差を四分位範囲といわれて、ここで出てきているものは、さっきの年収の話ではないですが、外れ値が多いようなもののばらつきを出すときに好まれる方法です。
外れ値の影響を受けにくいばらつきの指標はこれです。身長の例でいうと、さっきのこれでいうと、最小値が144cm、最大値が193cm、第3四分位数、つまり全体の上から25%の身長は175cm、下から25%の人は167cm。この四分位範囲というのを計算してあげると8。それぐらいばらついていますよ。この範囲が広がれば広がるほどばらついていると考えることができます。範囲に関してもそうです。最大と最小の間がどれだけ開けば開くほど分布としてはばらついているので、そういった指標になります。
こういう範囲を示すときによく使われるのが箱ひげ図というものです。見たことはあるかもしれませんが、これが箱です。箱とひげ、にょろんと伸びているもの。この真ん中の太い線は中央値を表していて、さらにそこに×印とか点で平均を表したりすることもあります。この箱の上側は第3四分位です。これは175cmぐらいだったかな。第1四分位はこういうふうに出てきています。さらに外れ値を一応、出すためにひげというのが書いてあります。第3四分位プラス1.5×四分位範囲とやってあげたのがこのひげのところです。これより外側にあるものは外れ値とみなそうというふうにします。下側も同じです。第1四分位から1.5×四分位範囲を引いてあげたりするというのが外れ値の境界として出てきます。
実際には量的変数のばらつきを表すときによく使われるのがこっちのほうです。標準偏差とか分散というものです。平均値とデータの差を偏差というんですが、つまりこの中のテストの点数で平均点が70点のテストで61点を取った人の偏差は-9。偏差の2乗を足し合わせてケース数で割ってあげると分散になります。分散の平方根、ルートを取ってあげると標準偏差になります。一般的にはこういうばらつきの指標を出すときは、量的変数の分布を要約するときは平均値と標準偏差を出すことが多いです。
それから標準偏差を使って、標準化をして標準得点を出したり、偏差値を出したりすることができます。皆さんも高校生とか中学生とか、受験のときに偏差値が模試のときに出ていたと思うんですが、その仕組みというのが実はあのときはまだ偏差値が上がったり下がったりで一喜一憂をしていたと思うんですが、それがこういうからくりで出ていたというのがここで出てくるんですが、何のためにやっているかというと、平均とか分散とか単位の異なるデータ、つまり模試であれば、それぞれに第1回代ゼミ模試と第1回駿台模試は平均点が違いますし、分散、ばらつき、受験生のレベルも違うのでばらつきが違う。
それをできるだけ比較できるようにしてあげよう。つまり代ゼミの模試で取る60点と駿台で取る50点は違うということです。それをできるだけ比較ができるようにしようということでやっているのが標準化というものです。これは模試の点数以外にも実際には皆さんの研究でも使えることでもあるんですが、標準化という考え方です。単位とか平均点の分散が違うものを比較できるようにするという考え方、標準化というのがあります。何をやっているかというと、異なる変数間で平均と標準偏差が同じになるように変換してあげる。
じゃあ、これをどうやってやるかというと、平均をゼロにして、ゼロ以外にもあるんですが、標準偏差が1になるように変換してあげる。どうやってやるかというと、それぞれの値から平均を引いてあげると平均がゼロになります。全てのデータから、つまりこの点数から平均点70点を引いてあげるとゼロになるというのは分かりますよね。イメージできますよね。今、平均点が70点なので、このデータ全体が70、Aの人からも70を引いて、Bの人からも70を引いてあげると、あげたものの平均を取るとゼロになります。さらにそこら標準偏差で割ってあげると、標準偏差も9.8なので、標準偏差は1になります。
そうやって出してあげたのが標準得点というものです。偏差値というのは標準得点を使って50が平均になるように。つまり50+標準得点×10というので出していくということになっています。なので偏差値が60の人は平均よりも1標準偏差だけ、点数が高かったりというのを表していますし、偏差が40の人は平均よりも1標準偏差、得点が低かったということになります。こんな感じですね。
さっきのものでいうと、標準得点というのは、それぞれの値から平均を引いて標準偏差で割ってあげたのがこの標準得点というものになります。懐かしいですね、偏差値。
ここで、何か分からないとか、ついていけないという人がいるかもしれないんですが、何か質問とかある人はいませんか。ときどき皆さん、大学院に入ったり、久しぶりに統計に触れるために例えばルートが分からないとか、2乗が分からないというような人もいるかもしれませんが、そのあたりは大丈夫ですか。今ならいくらでも。特に偏差値、標準偏差、分散というのは非常によくこれから出てきてきますので、統計解析をする上で、ばらつきとか分散はすごく大事な集団を扱うわけですから、大事な数値というか、値になってくるんです。これはいいですかね。何か分からなければ、また後で米倉先生なりにいろいろ聞いてみてください。じゃあ、続きをお願いします。
ということでここまでが1つの変数と集計したりとか、要約値を出して、集団の特徴というのを出していくというときにする基本的な処理でした。
統計講義動画
- 第1章 イントロダクション:データの作り方
- 第2章 記述統計と推測統計、データの型
- 第3章 1変量の集計
- 第4章 2変量の集計
- 第5章 推定と検定
- 第6章 パラメトリック検定とノンパラメトリック検定
- 第7章 パラメトリック検定
- 第8章 ノンパラメトリック検定
- 第9章 重回帰分析その1多変量解析の基礎
- 第10章 重回帰分析その2回帰分析の多変量バージョン重回帰分析
- 第11章 重回帰分析その3重回帰分析の応用
- 第12章 因子分析その1尺度による潜在変数の測定
- 第13章 因子分析その2探索的因子分析の基礎
- 第14章 因子分析その3因子の回転と解釈
- 第15章 多変量解析 ロジスティック回帰分析
- 第16章 多変量解析 構造方程式モデリング
統計コンテンツクイズ
設問 3-1-1
ある学校で20名の学生を対象に統計学の試験を行った結果、表1のような結果を得た。得点の算術平均値はどれか。
表1.試験の得点
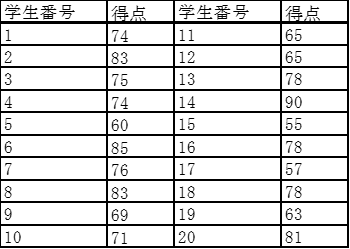
すべての身長を足し合わせて10で割ればよい。
(74++83+…+78+63+81)÷20=73点
設問 3-1-2
表1の得点の標本分散に最も近いのはどれか。
各人の得点から問11で求めた得点の平均を引き、2乗したものを足し合わせたもの(=偏差平方和)を人数で割ればよい。
(1+100+4+…+25+100+64)÷20=1784÷20=89.2
設問 3-1-3
他の科目とバランスをとるため、得点調整を行うことになった。得点調整は全学生の点数に一律に2点を加点するものであった。得点調整後の得点の平均と標準偏差の組み合わせに最も近いのはどれか。
平均点は75点
得点の標準偏差は√89.2=9.444≒9.4
平均はデータに定数を足すと定数分増えるから、全学生の点数に一律に2点加点すると平均も2点上がる。したがって、得点調整後の平均点は73+2=75点。
標準偏差はデータに定数を足しても変化しないので、得点調整後の標準偏差も9.444≒9.4
設問 3-1-4
試験の得点の分布をグラフで表したい。適切なグラフはどれか。
量的変数の分布を表すグラフとして適当なものとして、ヒストグラムや箱ひげ図がある。この中ではヒストグラムが適切である。
設問 3-1-5
表1のデータを集計して以下のような度数分布表を書いた。得点の30パーセンタイル値が含まれる階級はどれか。
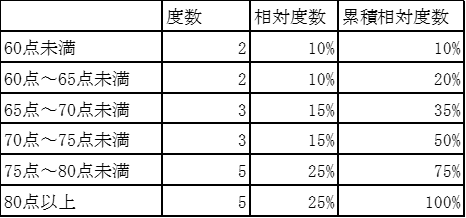
30パーセンタイル値は全データを小さい順に並べた時に下から30%にあたるデータの値である。累積相対度数が初めて30%を超える階級に30パーセンタイル値があるはずである。