第15章:多変量解析 ロジスティック回帰分析
ナレーション原稿
米倉 こんにちは。講師の米倉です。今日は、ロジスティック回帰分析についてお話をしていきます。今回の内容ですけれども、ロジスティック回帰分析についてなぜ必要なのかと。ここはロジスティック回帰分析で変数間の関連をどのように見ていくのかというところ。あとは、結果を論文で示したりする時に、どのように示すのかというのと、あとモデルの当てはまりの指標や、変数の選択の仕方、必要なサンプルサイズというのと、ロジスティック回帰分析での3カテゴリ以上の目的変数の扱いについてお話をします。
まず、ロジスティック回帰分析とは、どういった分析なのかというところで概要についてお話をします。ロジスティック回帰分析は二値データや確率などのデータを目的変数とした回帰分析です。二値データや確率などデータというのはどういうものかというと、疾患、癌があるかどうか、あるいは糖尿病の有無だったり、高血圧の有無のような疾患の有無だったり、要介護認定をされているかどうかだったり、有病率というような、二値データや確率などのデータを目的変数とした回帰分析が、ロジスティック回帰分析ということになります。
目的変数が二値データや確率データなだけで、考え方が重回帰分析などの一般線形モデルと同じです。説明変数の選択や投入の仕方は、回帰係数の解釈の考え方もほとんど共通しています。回帰係数の解釈については、回帰係数の値というのは、他の変数の値を固定して一つの変数だけ変化させた時の、目的変数との関連性の強さを表しています。
ただし、ロジスティック回帰分析では回帰係数の値というのは、説明変数1単位あたりの目的変数の変化量ではなくて、対数オッズというものの変化や、オッズ比として解釈するという点が少し違っています。また、質的変数を説明変数として使うときには、ダミー変数を使うというところも、一般線形モデルですね、重回帰分析などと同じです。
なので、重回帰分析についての動画をまだ見ていないという方は、先に重回帰分析についての動画を見てからこちらを、この動画を見ていただいたほうが学習はスムーズに進められると思います。
ロジスティック回帰分析はなぜ必要かというところなんですけれども、重回帰分析などの一般線形モデルでは、残差にこの3つの仮定をおいているわけですね。1つは、正規分布に従うというのと、互いに独立であるということと、あとはグループ間で分散が等しいという、3つの仮定がおかれています。
この制約が満たされていないと誤った結果になってしまったり、検定の結果が不正確になるということや、検出力、母集団で関連があったとしても関連がないというふうに判断してしまう可能性が高くなってしまうということです。検出力の低下というものだったり、モデルで予測する値がありえない範囲になったりするというようなことが起こります。
特に確率や割合、比率のデータがマイナスになったり1を超えたりするということで、定義上、確率や割合というのは0から1の値を取るわけですけれども、その範囲を超えてしまう、マイナスになってしまったり、1を超えてしまったりするということが起こってしまいます。なので、制約を満たさないデータというのは、一般線形モデルで扱うのは不適切だということになります。
ではこの二値データや確率データをどのようにして扱うかというと、二値データの例は先ほどお話ししましたが、疾患の有無だったり、基準を超えるか超えないか、何かスクリーニングの尺度や検査などの基準を超えるか超えないかだったり、あと一定期間内のイベントの発生です。1年間に要介護認定を受けるかどうかだったり、心筋梗塞を発症するかしないかというようなものは、二値データの例です。
そのままでは2値しかとらない、あるかないか、病気か病気でないかとか、要介護認定されたかされてないかというような2値しか取らないので扱いにくい。なので、この2値になる、2値のどちらかというのが、データとして観測されるわけですけれども、その2値を決める背後に確率、どちらになるかというのを決める確率というのを考えてあります。その確率をモデルに当てはめるということを考えるわけです。
その「確率」というのが一定の基準を超えれば「有り」、超えなければ「なし」が観測されるというふうに考えるというのが、この二値データの扱いの考え方の基本です。この確率のモデル化の仕方、数式に落し込む方法というのはいくつかあって、ロジスティック回帰分析というのは、確率と説明変数の関係をロジスティック関数という関数でモデル化をしています。
他にも正規分布の累積分布関数でモデル化したプロビットモデル、プロビット回帰分析というようなテーマもあります。今回は扱いませんけれども、そういった二値変数の扱いとしてプロビットモデルというのがあるのは、知っておいてもいいかもしれません。
イメージとしては、0、1の2値の変数のままだけではなくて、これを確率0から1に収まるように「確率」に置き換えてあげる。置き換える時に使う関数というのが、ロジスティック関数というものになります。
ロジスティック関数というのはここに出てる関数なんですけども、イベントが起こる確率というのを、ロジスティック関数でモデル化することで回帰モデルを作るというのが、ロジスティック回帰分析というものになります。
ロジスティック関数というのは、この関数ですね、xが-∞から+∞の範囲で、yが0から1の範囲を取るので、確率をモデル化にするのにちょうどいいと。確率は0未満にもならないし、1を超える値というのも取らないので、ちょうどモデル化に都合がいいわけです。
目的変数が1になる、何かイベントが起こる確率、病気になる確率だったりとか、介護認定をされるような確率、その確率というのをこのように説明変数と切片の関数でモデル化してあげるということになります。
これをぜひ変形してあげると、このように、このように、最終的にはp/(1-p)です。つまり病気やイベントが起こるか起こらないかの。オッズの対数を取ったものです。このlnというのは自然対数です。自然対数でこの対数オッズというのを目的変数にした重回帰分析のように扱うことができます。
ロジスティック回帰分析では、このようにロジスティック関数でイベントが起こる確率をモデル化してあげる。変形すると、このように対数オッズ=β0+βXというような形に変換することができるんですね。
このロジスティック回帰分析で関連を、目的変数と説明変数の関連の強さというのを見る時には、オッズ比というものを用いて解釈することが多いです。オッズ比というのは、疫学などでも出てきて、基礎教育などで学んだ人もいるかもしれませんが、オッズ比というのはオッズの比です。オッズというのは何かというと、あるイベントが起こる確率と、起こらない確率の比です。
オッズ比の解釈としては、説明変数が量的変数の場合は、説明変数の値が1増えると、オッズ、このイベントが起こるオッズというのは何倍になるかということを表しています。質的変数が説明変数の場合は、参照カテゴリに比べてオッズが何倍になるかというのを表しているのが、オッズ比の解釈だということになります。
ロジスティック回帰分析の回帰係数からオッズ比というのがどういうやって出てくるかというのを表した式がこれで、このXの値ですね、説明変数の値を1だけ変化させたものと、元のものというのを引き算をしてあげると、このように最終的に出てきた係数の指数を取ってあげると、オッズの比になるということから、オッズ比というのを求めることができます。
この導出の仕方については、特に知らなくても結果が見れれば最低限、結果を解釈できますけれども、ここらへんの導き方についても知っておくと、だいぶイメージしやすくなるのではないかなと。
ロジスティック回帰分析を行った結果というのを論文などの表で示すと、このような形で示されたりします。この表というのは、東日本大震災によって家屋被害や同居者の死亡とか行方不明、あと失業の状況と、あと被災2年後、東日本大震災から2年後の被災者の精神健康の状態の関連というのを分析したものです。
これは男性で、この精神健康が不良であるというものに関連する要因というのを、いろいろ見たものなんですけれども、この結果を見てみると仕事の状況、家屋被害とか同居者の死亡・行方不明・失業というのは、震災2年後の精神健康とは有意な関連というのはなかったんですけども、現在、2年後時点の社会経済的な状況、仕事の状況、仕事をしていない人では仕事をしている人に比べると、精神健康は不良であるというオッズ比というのは高いということです。
仕事をしていない人のほうが精神健康は不良になりやすいというのと、あと暮らし向き、経済的な暮らし向きは普通の人と比べると苦しい、というふうに回答した人では、精神健康は不良であるという人が多いということが分かります。
それ以外にも病気の有無、精神疾患の有無だったり、あとは元々精神健康があまり良くなかった人というのは、2年後も精神健康が悪いというようなこともここから分かるということになります。
先ほどの表には出てきていませんでしたけれども、分析を統計ソフトなどでした時は、それ以外の多重共線性を各チェックしたり、オッズ比の信頼区間のチェックしたりというところも、必要になってきます。多重共線性は重回帰分析のところでも出てきましたけれども、変数間の相関やVIFと分散拡大要因などを確認すればいいということになります。
SPSSというソフトでは、ロジスティック回帰分析のオプションには、この多重共線性の診断指標を出す機能はないですけれとも、線形回帰のオプションで出力すれば出てきます。
それからオッズ比の確認ですけれども、信頼区間が広すぎていないかとか、信頼区間の上限が大きすぎないかというようなところを見ます。大きすぎたり広すぎる場合は、質的変数の参照カテゴリのサンプルサイズが少なかったり、イベント数が少ない場合というのがあります。
参照カテゴリをサンプル数が多いカテゴリに変更したり、カテゴリを併合したりすると改善する場合もありますので、オッズ比の値だったり、信頼区間のチェックというのもしたほうがいいということになります。
それからロジスティック回帰分析の適合度、当てはまり要素をどの程度うまく予測できているかというのの指標はいろいろなものがあります。ここに挙げてあるのが、疑似決定係数というのと、情報量基準、AUC(Area Under Curve)と適合度の検定というところが、よく使わる適合度の指標や検討法です。
疑似決定係数というのは、重回帰分析などの一般線形モデルでの決定係数、R2、R-squaredと同じようなものです。いろんな種類があって、Nagelkerkeの決定係数やCox-SnellのR2とか、McFaddenの決定係数などがあります。NagelkerkeはCox-Snellを0から1に収まるように補正したものというものです。ある一定、幾つ以上だったら当てはまりがいいか、いいというような基準というのはないので、モデルを比較する時などに使うというのは、疑似決定係数の使ういいところかなというふうに思います。
それから情報量基準というもので、当てはまりを評価することもできます。これも疑似決定係数と同じように複数のモデルを比較する時に使うと。この情報量基準、AICとかBICというようなものは値が小さいほど、低いほど少ない変数でよく予測できているということを表しているというので、値が小さいほど良いというような指標です。
それからAUCやC統計量というものなんですけれども、これは観測値とあとモデルによって予測された確率というのを元に、ROC曲線を書いた時の曲線の下の面積、どの程度うまく予測できているかの指標というのが、AUCというものになります。値としては0.5~1までの間を取って、0.5~0.7はあまり良くなく、0.7~0.9は適度、0.9以上は良好な当てはまりであることを表すというふうに言われています。
それから当てはまりが良いかどうかというのを検定することもできて、その検定の一つはHosmer-Lemeshowの検定というものになります。帰無仮説は「モデルによる予測が観測と一致している」、つまり当てはまりが良いというのが帰無仮説ですので、検定をして有意になれば適合しているとは言えない。有意でなければ適合していると。適合していないとは言えないですね、厳密に言うと。でなければ、適合していないとは言えないというふうに、解釈することができるということになります。
それからロジスティック回帰分析も多変量解析ですので、説明変数を選択するんですね。どの説明変数を使うかというのを選ぶということが必要になってきます。選び方は重回帰分析のところで出てきた方法と基本的には同じで、研究の仮説に従って選ぶというのは、学術研究では原則となります。なので、先行研究をよくレビューをして、どんなものがすでに明らかになっていて、何が新しいというところをきちんと押さえていく必要があるということです。
それから因果推論を行う際には、非巡回有向グラフ、DAGと呼ばれといますけれども、このDAGによる視覚化と整理をすることで、どんな変数で整理をすればいいかというのを考えることができますので、これも有効かなと思います。
それから回帰係数が有意ではない変数でも、仮説モデルにあったら残す。有意か有意でないかという結果をちゃんと出すというのも大事なことになってきますので、有意じゃないからといって、変数を除外してしまうということはしないほうがいいです。
それと同じようなことをやってしまうのは、ステップワイズ法です。ステップワイズ法は使わないほうがいいというのは、いろんなところで言われています。ステップワイズ法というのをP値を基準に変数を選択する方法で、欠点としては有意な変数が残って有意でない変数は残らないということなので、注目していた、せっかく仮説を立てて注目していた変数だったり、本当はそれに関連がある、母集団では関連がある変数が残らないということもあります。
それからαエラーです。たまたま関連が出てしまうということもありますので、本当は関係がない変数なのに残ることもあると。そういった変数が出てきてしまうと、なぜそういうふうに関連しているのにというのを、解釈できない結果というのが出てきてしまうので、困ってしまうということが起こります。
それからオーバーフィッティングが起こるというのも問題というふうに言われていて、この分析に使ったデータへの当てはまりはいいんですけども、別のデータ、つまり他のデータに応用することはできないというような結果が出てしまうことも起こるわけです。なので、ステップワイズ法というのは使わないほうがいいということは言われています。
あとは分析の対象となるデータです。どれぐらいデータ、対象者の数が必要かというところなんですけれども、古典的に使われてきた基準というのはEPVとEvent per variableというものを元に決めるという方法です。このEPVというのは説明変数1つあたりのイベント数のことで、古くはこのEPVが10以上になるようにデータを集めるといいですよというふうに言われていました。
どういうことかというと、説明変数を10個使いたければ10×10ですね、100ケースのイベントが必要となってくるので、そのイベントが起こる確率、母集団での有病率だったりとか、発生確率というのが20%だとすると、この20%、全体では100÷0.2の500ケース集めれば100ケースのイベントが期待できるので、500ケース集める必要があるよというふうなことを考えるということです。
ただ、この10以上というのは目安で、いろんな条件次第で10よりも小さくていいというふうにするものだったり、10では不十分とするものというのもあります。それからロジスティック回帰モデル分析で予測モデルを構築するという場合では、EPVだけを元に決めるのは不十分というふうに言っているものもありますので、詳しくはここらへんに挙げた論文を確認していただいて、どんなふうにして決めればいいかというところを、知っておいてもらうといいかなというふうに思います。
探索的な研究の場合は、EPVをベースにある程度の数を見積もってどれぐらい最低限必要かというのを、見積もっておくといいかなと思います。あとは、臨床試験など閉鎖的な研究の場合には検出力を元に決めるということで、有意にしたい回帰係数の大きさなどから決めるというふうな方法もあります。
ここまでが二項ロジスティック回帰分析です。通常のロジスティック回帰分析のお話になります。
ここからはロジスティック回帰分析の拡張ということで、3個以上、3値以上の選択肢のデータを扱う、多項ロジスティック回帰分析や順序ロジスティック回帰分析というもののお話です。
多項ロジスティック回帰、順序ロジスティック回帰というのは、二項ロジスティック回帰分析の拡張で3値以上の選択肢のデータも扱うことができます。多項ロジスティック回帰分析と順序ロジスティック解析分析の違いなんですけれども、多項ロジスティック回帰分析は目的変数の選択肢に順次を付けられない変数を扱う分析というのは、多項ロジスティック回帰分析です。
要は名義変数を目的変数とした回帰分析をすることが、この多項ロジスティック回帰分析です。例えば、職種、技術職なのか、事務職なのか、営業職なのかというふうに、特に順序が付けられないようなものを目的変数として扱うモデルが多項ロジスティック回帰分析というものになります。
それから順序ロジスティック回帰分析というのは、目的変数の選択肢に順序を付けることができる変数を、目的変数として扱うものです。順序変数を目的変数としたロジスティック回帰分析となります。
例としては、健康状態の自己評価といったもの、年収をグループに高中低というふうに分けたり、あとは要介護度のように要介護1、要介護2、要介護3というような形で、順序は付けられるけれども、間隔は等しいとは言えないというようなものを目的変数にする場合というのが、この順序ロジスティック回帰分析というものになります。
ただし、順序変数の場合は量的変数とみなして重回帰分析をしたりすることもありますので、どちらを選ぶかというのは、その変数のカテゴリの数であったりとか、間隔が等しいとみなせるかどうかというようなところを、総合的に判断してどちらを使うというのを考えていければというふうに思います。
考え方、この多項ロジスティック回帰分析と順序ロジスティック回帰の考え方なんですけれども、基本的には2項ロジスティック回帰分析と同じで、どの選択肢が選ばれるかというのを決める潜在的な「確率」というのを使ってモデル化をしています。多項ロジスティック回帰は目的変数の基準となるカテゴリ、参照カテゴリと注目するカテゴリの選択を決める「確率」というのを比較します。説明変数の値によって、参照カテゴリと注目するカテゴリのどちらが選ばれやすいかというのが、この多項ロジスティック回帰分析で分かるわけです。
今、その参照カテゴリか注目するカテゴリの選択を決める「確率」に、説明変数が与える影響というのを見ているということです。なので、目的変数の参照カテゴリの選び方で何と何を比べるかというのが変ります。これが多項ロジスティック回帰分析の特徴です。
説明変数の回帰係数(オッズ比)というのは、説明変数の値が1大きくなると、参照カテゴリと比べて注目するカテゴリは、どの程度選ばれやすくなるのかというのを表しているというのが、多項ロジスティック回帰分析のオッズ比、回帰係数の解釈ということになります。
順序ロジスティック回帰分析では、選択肢全体に共通する特性というのに説明変数が与える影響を見るということで、説明変数の回帰係数(オッズ比)というのは、説明変数の値が1大きくなると、どの程度順序が上のカテゴリが選ばれやすくなるというのを表している。
何となくのイメージですけれども、多項ロジスティック回帰分析(多項ロジットモデル)というのは、ペアごとに基準となるカテゴリと注目するカテゴリの間というのを比較するというのが多項ロジットモデル。順序ロジットモデルでは、カテゴリ群全体で比較をして、階段のように表現していきますけれども、この順序を上げるような方向に説明変数を働くか、それとも下げる方向に働くのかというのを見るというのが、順序ロジット解析式のイメージということになります。
多項ロジスティック回帰分析の例ですけれども、この論文では東日本大震災の被災地域住民を対象とした調査で、精神健康度を「問題なし」「軽度の異常」「重度の異常」の3段階に分類して、健診の受診状況との関連を見たものです。これは男女別に上段が男性、Maleと書いてあって、下段がFemaleと書いてありますけれども、男女別に年齢調整のみを行った結果というのと、多変量調整を行った結果というのが示されています。このAge-adjustedというのが年齢調整のみを行ったもので、Multivariate-adjustedというところには、この行には多変量調整を行った結果が出ていると。
ただし、今までよく見てきた回帰分析の結果と少し違って、健診状況、受診状況以外の変数と精神健康度の関連性というのは表では省略されていて、ここで示されているこの値というのは、健診受診状況、健診を受診していない人が、どれだけ精神健康度が悪くなるかというのを表しています。
例えば、この上段のMultivariate-adjusted、多変量調整をした結果のところを見ると、このMild、軽度の異常というのは健診を受診していない人ではMild、軽度の異常となる動きというのは1.69倍高い。このカッコの中に示されているのは、95%信頼区間ですので、95%信頼区間が1をまたがなければ5%水準で有意ということになので、有意にこの軽度の異常というのは、健診を受診していない人では起こりやすいということになります。
Severeというのは、重度の異常ということで、これも健診を受診している人に比べて健診を受診していない人では、この重度の異常というのは起こりやすい。ただ検定をすると、信頼区間が1をまたいでいますが、有意ではないということになります。
女性のほうは全て有意になっていて、女性のほうでは健診を受診していない人のほうが、軽度の異常のオッズ比というのは1.46なので、1.46倍オッズが高いと。つまり健診を受診していない人は軽度の異常というのになりやすいというのと、重度の異常のほうもなりやすいというようなことが、この結果から分かります。
もう一個は、順次ロジスティック回帰分析の例ですけれども、これは健康相談の必要性の認識というのを目的変数にして、対象者のいろいろな特徴との関連を分析したものです。オッズ比が1を超えているのは、必要性の認識が強くて、1未満であれば必要性の認識が弱くなる方向に関連をしている。
これを見てみると、例えば「家族関係にストレスがある」というふうに回答した人では、オッズ比は1.8なので、1.8でも有意になっていますので、この家族関係にストレスがあるという人は健康相談の必要性を必要というふうに、認識しやすい方向に関連していくということになります。
それ以外、下のほうについて見てみると、健康について相談したい医療者、必ず医師がいいというふうに回答した人はオッズ比が0.53で有意なので、このような回答をした人というのは、健康相談の必要性や認識というのは低い、全く必要がないというふうに答える可能性というのが、高いというふうに見ることができます。
このような形で多項ロジスティック回帰や、順序ロジスティック回帰を使うことで、3カテゴリ以上、3値以上の質的変数というのを目的変数にした回帰分析というのを行うこともできるということで、ロジスティック解析分析では、この質的変数全般を目的変数とした回帰モデルというのを作って、説明変数との関連を見るということになります。
ロジスティック解析分析については以上ということになります。今回はこれで終わりにしたいと思います。(終了)
統計講義動画
- 第1章 イントロダクション:データの作り方
- 第2章 記述統計と推測統計、データの型
- 第3章 1変量の集計
- 第4章 2変量の集計
- 第5章 推定と検定
- 第6章 パラメトリック検定とノンパラメトリック検定
- 第7章 パラメトリック検定
- 第8章 ノンパラメトリック検定
- 第9章 重回帰分析その1多変量解析の基礎
- 第10章 重回帰分析その2回帰分析の多変量バージョン重回帰分析
- 第11章 重回帰分析その3重回帰分析の応用
- 第12章 因子分析その1尺度による潜在変数の測定
- 第13章 因子分析その2探索的因子分析の基礎
- 第14章 因子分析その3因子の回転と解釈
- 第15章 多変量解析 ロジスティック回帰分析
- 第16章 多変量解析 構造方程式モデリング
統計コンテンツクイズ
設問 15-1
二項ロジスティック回帰分析の目的変数として適切なのはどれか。
二項ロジスティック回帰分析の目的変数として適切なのは、2値の質的変数である。選択肢の中で二値の質的変数なのは、「b。調査時点で糖尿病であるかどうか」のみで、他は量的変数である。
設問 15-2
順序ロジスティック回帰分析の目的変数として適切なのはどれか。
順序ロジスティック回帰分析の目的変数は順序変数である。選択肢のなかで順序尺度のものは、「d. 疾患の重症度を軽度、中等度、重度として評価したもの」のみである。a、cは量的変数、bは名義変数である。
設問 15-3
多項(名義)ロジスティック回帰分析の目的変数として適切なのはどれか。
多項(名義)ロジスティック回帰分析の目的変数は3カテゴリ以上の名義変数である。選択肢のなかで3カテゴリ以上の名義変数は、「b.どの治療方法(手術、放射線、抗がん剤)が選択されるか」のみである。それ以外は量的変数である。
設問 15-4
地域住民を対象に調査を行い、精神健康が不良であることを目的変数としたロジスティック回帰分析を行った結果、下表のようになった。この結果についての説明として、誤っているものはどれか。
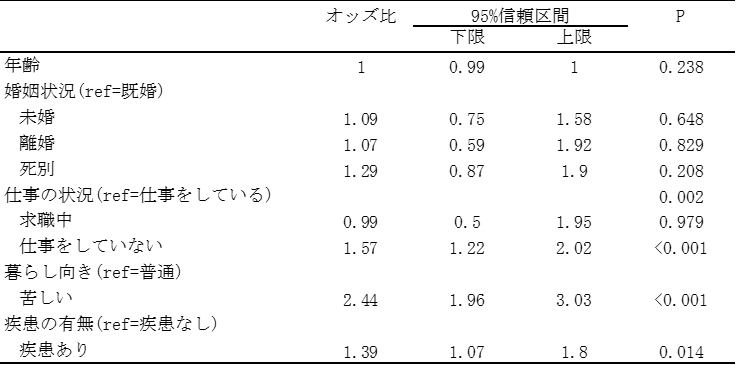
ref: 参照カテゴリ
「仕事をしていない」のオッズ比は1.57でP値は0.001未満なので、参照カテゴリである「仕事をしている」者と比較して、有意に精神健康が不良であるオッズが高く、精神健康が不良になりやすいことがわかる。したがって、bの「精神健康が不良になりにくい」というのは誤り。