第11章:重回帰分析その3重回帰分析の応用
ナレーション原稿
(スライド番号38から)
米倉 今やったですね、このモデル間の比較ですね、複数の説明変数のセットで、説明変数のセットを変えて分析をしていく重回帰分析のことを階層的重回帰分析というふうに呼ぶこともあります。階層的重回帰分析ではですね、投入する説明変数というのを順次追加していって、偏回帰係数の変化というのを見るということをします。これによって、複数の説明変数を含む、異なるセットの説明変数を含むモデルを比較することができて、それによってですね、説明変数間の相互作用とかを見たり、目的変数にどうように関連しているのか、影響を与えているのかというのを推測することができると。この考え方をですね、さらに発展していって、複数の重回帰分析というのを同時に、連立方程式のように立てて、全部まとめて偏回帰係数を求めてあげようというふうに発展していったのがパス解析というですね、構造方程式モデリングというものになります。これは、この授業ではお話しませんけれども、構造方程式モデリングの話は、教科書のほうに書いてあると思うんで、関心があればですね、見ていてください。
それから、階層的重回帰分析の例ですけども、このようなものですね。モデル1とモデル2とありますけども、最初のモデル1では、配偶者の部分というのが入っていなくて、年齢と就業の有無だけが説明変数として入っていると。これも目的変数はさっきちょっと出てきた、食に関する主観的QOLで、食に関する、食事の満足度というか、食生活の充実度のようなものと考えてください。これが、見てみると、年齢と就業の有無だけの関連を見ていると、就業の有無というのは、有意にですね、この食に関するQOLというのと、正の関連をしていて、就業している人のほうがこのQOLが高いという結果になっていました。ここにですね、配偶者の有無というのを追加するとどうなるかというと、結果が大きく変わるわけですね。どう変わるかというと、就業の有無の関連というのはほとんどなくなってしまう。標準化係数がほぼ0になってしまって、検定の結果もまったく有意じゃなくなっていますね。この2つを比較することで何がわかるかというと、実はこの就業の有無というのは、直接この食に関する主観的QOLと関連していたわけではなくて、配偶者の有無が裏にあってですね、関連があるように見えていたわけですね。これは交絡しているのか、媒介しているのか、これだけではわからないですけども、就業をしている人のほうが配偶者がいる可能性が高いと。なので、配偶者の有無と就業の有無というのは、けっこう関連が強いわけですね。さらに配偶者がいるほうが、この食に関する主観的QOLが高いというふうに出ているので、配偶者がいたほうがいいと。これは男性だけに今絞っているので、男性に配偶者がいると、食生活が充実すると。一方で、配偶者がいるいかどうかという条件が同じであれば、働いていようが働いてなかろうが、この食に関する主観的QOLというのは変わらないというふうに見ることもできるわけですね。ということで、この3者の関係、3者と、この食に関する主観的QOLの関係というのは、こういうふうにですね、階層的重回帰分析をすることで、この就業の有無がどのようにして、食生活の充実度に関連しているのかというのを見ることができます。
ここからはですね、モデルの全体としての評価の話を少ししていきます。回帰分析のときに、決定係数の話をしましたけれども、この決定係数というのは、どれだけ残差が少ないというのを評価することで、回帰式がどれだけよく目的変数のばらつきを説明できているかというのを評価しているものでした。決定係数は0から1までの値を取って、1に近いほどあてはまりがいいということを表しているというようなものを思い出してもらえればと思います。重回帰分析のときに困ってしまうのがですね、この決定係数というのは、説明変数が多くなると自動的に多くなっていって、あまり意味のない、説明力が高くない変数でも、最終的にはですね、サンプルサイズと同じだけ説明変数を加えてしまえば、決定係数が1になってしまうという欠点があります。あとは、この説明変数が多いほど、決定係数としては有利なので、説明変数の数が異なる重回帰分析の結果のあてはまりを比較するときに、フェアじゃなくなってしまうわけですね。なので、この説明変数の多さというのを考慮して比較するための指標というのは、自由度調整済みの決定係数というもので、これの計算式としてはですね、さっきの決定係数の計算を少しアレンジして、もともとは残差平方和を目的変数の平方和で割っていたわけなんですけども、このそれぞれに、残差平方和のほうには、このp、説明変数の数が多ければ多いほど、この分子のほうは大きくなるようなペナルティーがあると。目的変数の平方和のほうは、サンプルサイズで割ってあげるというようなことをしてあげています。なので、この分子のほうに説明変数の多さ、説明変数が多くなると、分子が、つまり残差の平方和の重みが重くなるような修正をかけてあげることでですね、その説明変数の多さを考慮して、説明変数の数が違う重回帰分析の結果でも比較できるようにしているものというのが自由度調整済み決定係数というものになります。なので、重回帰分析でですね、あてはまりを比較したいというときには、こういう指標を使ったりするということもあります。
それから、重回帰分析になってくるとですね、説明変数が複数になることによって起こってくる問題として、多重共線性というものの問題が出てきます。これは、多重共線性というのはいったい何かというと、説明変数として似たもの同士ですね、複数の相関が高い変数を投入することで起きてしまう現象です。これはどういうときに起こるかというと、説明変数間の相関が高い場合や、ある説明変数がほかの説明変数で説明されてしまう。一次従属とか、線形従属のような関係になっているようなときに、この多重共線性というのが起こると。主な症状ですね、多重共線性が起きているときに出てくる結果の異常としては、まずは一番ひどいときだと、回帰係数などの値が出てこない。推定できないというようなことが起こったり、あとは推定された回帰係数が理論からは想定されないような値になると。符合が逆になるような結果が出てきてしまったり、標準誤差が大きくなって、検定が有意になりにくくなる。推定の精度が悪くなるというようなことが起こります。この多重共線性が起こっているかどうか、もしくは起こりそうかどうかというのを評価する方法、チェックする方法としては、1つは、説明変数間の相関係数を確認することで、相関が高いもの同士というのを説明変数として同時に投入しないように注意をするというのが1つ。もう1つは、この多重共線性を評価するための指標というのがあって、分散拡大要因という指標があります。この分散拡大要因というのを計算して、その値が5から10を超えていたら、これは分野とか等によって変わってくるんですけども、おおむね5とか10とかを超えていたら、多重共線性が起こっている可能性があるというふうに疑うぐらいの水準というのはこれぐらい。これでですね、多重共線性が起こってしまったというときには、対処方法としては、相関が高い説明変数同士のどちらかを除去して、1つだけにするという方法。もしくは、除去するのではなくて、合成してしまうという方法もあります。合計点を出したりとか、あとは来週やるような因子得点の点数を出したりとかして、それをまとめて、相関の高い変数同士をまとめて、合成変数として扱うというような。サンプルサイズが大きければですね、標準誤差が大きくなっても、十分検定は有意になるので、サンプルサイズを増やすというのもこの多重共線性の問題の対処方法になります。ただし、解析する段階ですね、分析をする段階では、サンプルサイズを増やすことは通常できないので、サンプルサイズのほうを増やすというのは、あくまでも分析をする前ですね、研究前の段階でできるだけ多く取っておくというようなことをすると。
特にですね、多重共線性の問題が起こりやすいのは、交互作用ですね、つまり修飾、効果の修飾が起こっているかどうかというのを見るときに注意をする必要があります。交互作用ですね、交互作用項の変数をそのままかけ算をして重回帰分析に使ってしまうと、交互作用項とあともともとのこの交互作用の要素ですね、この例で言うと、これは年齢と体重の交互作用というのをですね、入れているんですけども、これは、モデルとしてはあまり意味がないんですが、こういう交互作用のもととなる変数と、交互作用項のあいだに相関がものすごく高くなってしまって、このようにですね、VIFというのが分散拡大要因なんですけども、この値が、さっき10を超えたら多重共線性に注意が必要だとかという話をしていましたけども、もう優に10を超えてしまっているわけですね。こういったことが起こるので、交互作用項を構成する量的変数は、中心化ですね。平均を引くか、もしくは標準化の平均を引いたうえで、標準偏差で終わるというような操作をしておく必要があります。そうすることで、多重共線性が起こりにくくなるようにすることができるということですね。多重共線性が起こると、例えばなんですけども、これは、目的変数、従属変数が身長ですね。通常、身長が高いと、体重も重くなるわけなんですけども、この回帰係数の値を見てもらうとわかるとおり、体重が重い、体重が1キロ増えるごとになぜか身長が縮むというような係数が出てきています。このように、多重共線性が起こると、あり得ない、解釈ができないような回帰係数の値というのが出てくるというのが、症状の一つですね。なので、これが、注意が必要というか、こういったところは注意が必要になってくることになります。
それからあとは、分析結果のチェックとしてですね、これは実際に自分で分析をするときに気をつけるというか、確認をしたほうがいいということなんですけども、残差に関する前提ですね。最初のほうに、モデルの説明の最初のほうに、一回戻りますけども、重回帰分析というのは、誤差の分布の仮定ですね、この誤差の部分の仮定として、独立に正規分布に従っていて、等分散、すべての区間で等分散だというような仮定を置いています。その仮定がちゃんと満たされているだろうかというのを確認するためのチェックというのが、回帰診断というものです。残差が正規分布ですね、誤差が正規分布に従っているかどうかというのを確認するというのは、正規確率プロットというのを書くことで確立することができます。それから残差の等分散性というのと、独立性ですね。誤差の仮定にちゃんと従っているかどうかというのは、予測値に対して残差の値というのもプロットすることでチェックすることができます。それ以外に外れ値とか、影響点ですね。すごく大きな値とか、すごく小さな値によって、回帰係数が大きく変わってしまうということがあるので、そういった点がないかどうかというのもチェックして、もしそういうのがあった場合には、それを外したときに結果がどういうふうに変わるかというのを確認したりするということもあります。この外れ値とか影響点のチェック方法としては、Cookの距離とか、てこ比というのも見ることで、確認をすることができるということですね。
正規確率プロットというのは、こういうですね、実際の分析確率と、期待される正規確率というのを書いたもの。45度戦上ですね。この直線上に乗ってくれていれば、正規分布に従っているかどうかというのを確認することができます。プロットが直線上に並んでいれば、残差というのは正規分布に従っていると見なしてよさそうというふうに評価することができます。
それから予測値に対する残差のプロットというのはどういうものかというと、このX軸に予測値ですね、回帰分析で予測される値、予測する値ですね。つまり、一個一個のデータの説明変数の値に、実際のデータの値を代入していったものというのがこの予測値ですね。それから、残差ですね。残差というのは、それぞれの人のデータ、観測値と予測値の差を取ったものですね。残差、等分散性、独立性をこのプロットで確認することができるというのは、まず等分散性といのは、この上下への散らばり具合ですね。0を中心にしたですね、散らばり具合、上下への散らばり具合というのが、おおむね対称になっていれば等分散性というのは確認することができます。区間によってばらつきが違う場合には、等分散性が成り立っていないということを疑う。よくあるのは、予測値の値が大きくなればなるほど、分散は、残差がどんどんばらつきが大きくなってくるというようなことはけっこうあるので、そういったときには等分散性が成り立っていないことを疑うと。それから、残差のばらつき方に傾向がある場合ですね。波を打っているとかですね、規則性があるような場合には、独立性が成り立っていないことを疑う。独立性が成り立たないようなデータの典型的なものとしては、時系列のデータですね。同じ人に何回も調査をしたりして、調査とか実験をして集めたデータを回帰分析しようとすると、独立性というのが成り立っていないことが多いので、そういった結果が出る可能性があると。このグラフに関しては、上下対称にだいたいばらついていますし、特に何か規則性があるようにも見えないので、これも特に問題はなさそうだというのがわかります。
それからCookの距離とてこ比のプロットというのは、その値をですね、実際にグラフに書いてあげて、規定というかですね、値を超えるものがあるかどうかというのをチェックすると。これはプロットしなくても、値そのもののロス分布とかを見ることでも確認することができます。ここら辺でですね、特にてこ比のほうは、これみたいにですね、けっこう基準に引っかかるようなものが出てきたりとか、こっちではしていますけども、あまりこういう外れ値とか影響点とかというのをむやみに削除するというのも、結果をゆがめてしまうことにもなるので、データを削除するかしないかとかというのは、慎重にですね、判断する必要があるというふうに思います。
あとは重回帰分析をするときに、説明変数が複数あるわけですけども、その説明変数をどうやって選ぶかというのも、自分でですね、研究をするときには重要になってきます。原則としてはですね、自分の仮説に従って選ぶというのが原則で、ただやみくもに私の仮説はこうだというふうにやって、適当に選ぶというのは駄目で、先行研究のレビューをきちんとしたうえで、説明変数を選択するというのが大事になります。最近ではですね、因果推論、統計データから因果推論するというのは、最近はよく出てきて、今年のノーベル経済学賞とかでもですね、統計的な因果推論の話とかでありましたけども、因果推論をおこなうときには、非巡回有向グラフというものがあって、変数間の関連を矢印でつなげて、視覚化して、それのグラフのつながり方によって、どの変数を調整すればいいか、どの変数をモデルに含めればいいかとかというのを選択するのがですね、比較的簡単にできるというような方法があるので、そういうのを使ったりするのは、けっこう有効だというふうに言われています。それから、よくある教科書とかにも書いてあったりしたり、論文とかでも実際にやられていることが多くて残念なんですけども、回帰係数が有意じゃない変数を除外するというようなことは、基本的にはしないほうがよくて、仮説でちゃんとですね、モデルに含めるべきだというふうになっているのであればちゃんと残して、関連がなかったとしても、ちゃんと結果としては出すというのは大事なことになります。あとは、一応ソフトで一定の基準に従って選ぶということもできるんですけども、それでこの方法は学術研究でやっていると、あまりいい印象を持たれないということがあります。自分で仮説を持っていないというふうに言っているようなものなので、あとはここに挙げているステップワイズ法とか、変数増加法、変数減少法というのは、原理としては有意な変数が残って、有意じゃない変数は残らないというようなものになっているので、最悪ですね、もともと注目していた変数があるんだけども、ステップワイズをやったら消えちゃったとかですね、そういったこともあります。なので、逆に今、本当は関係がない変数が残るということもあって、あまりいいことはありません。なので、ステップワイズとかは、基本的には使うなというふうに言われています。ただ、使いどころがあるとしたらですね、目的変数に関連する、変数に関する情報がまったくないというときには有効なこともあるので、そういうときにはちょっと見通しをつけるという意味でやってみることはできるかもしれません。
それからあとは、これも実際に研究をするときに思い出してもらえればいいんですけども、サンプルサイズ、どれくらいデータを集めればいいかというのも、分析をするときにですね、考えることの一つです。大きな方針としてはですね、ちゃんと推定ができるかというような、推定の安定性のベースにした決め方というのと、あとは検出力ベースの決め方ですね、というのがあります。推定の安定性ベースであればですね、重回帰分析の場合は、説明変数の10倍ぐらいですね。説明変数の10倍のケースを集めれば、だいたいいいですよとか。あとは検出力ベースになってくると、より検証的なデザインのときに使うんですけども、サンプルサイズ計算用のソフトがあるので、それを使ってですね、計算をしてあげればいい。両方とも計算して多いほうを採用しておけばですね、安全というか、十分なサンプルサイズが得られて、事前にですね、どれぐらいデータを集めればいいかというのを、ある程度見積もっておくといいということは、最近では言われています。
今日はですね、重回帰の話をしてきたんですけども、話としてはこれぐらいで、これで終わりにしたいと思います。
統計講義動画
- 第1章 イントロダクション:データの作り方
- 第2章 記述統計と推測統計、データの型
- 第3章 1変量の集計
- 第4章 2変量の集計
- 第5章 推定と検定
- 第6章 パラメトリック検定とノンパラメトリック検定
- 第7章 パラメトリック検定
- 第8章 ノンパラメトリック検定
- 第9章 重回帰分析その1多変量解析の基礎
- 第10章 重回帰分析その2回帰分析の多変量バージョン重回帰分析
- 第11章 重回帰分析その3重回帰分析の応用
- 第12章 因子分析その1尺度による潜在変数の測定
- 第13章 因子分析その2探索的因子分析の基礎
- 第14章 因子分析その3因子の回転と解釈
- 第15章 多変量解析 ロジスティック回帰分析
- 第16章 多変量解析 構造方程式モデリング
統計コンテンツクイズ
以下の表は40代男性を対象に塩分摂取量と収縮期血圧を調査した結果をまとめたものである。
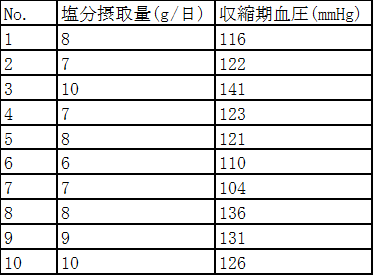
設問 11-1-1
このデータをもとに収縮期血圧と塩分摂取量の関連性を分析するため、収縮期血圧を目的変数、塩分摂取量を説明変数とした回帰分析を行った。その結果、切片は75.0、回帰係数は6.0となった。この結果からわかることはどれか。当てはまるものをすべて選べ。
収縮期血圧が目的変数、塩分摂取量が説明変数で、切片が75.0、回帰係数が6.0なので、収縮期血圧と塩分摂取量の関係は以下のようになっていることがわかる
収縮期血圧=75.0+6.0×塩分摂取量+誤差
回帰係数が6.0なので塩分摂取量が1g多いと収縮期血圧は6 mmHg高いことがわかる
以上を踏まえて各選択肢の正誤を検討すると以下の通り。
a.収縮期血圧と塩分摂取量には負の相関関係がある。
→誤り: 塩分摂取量の回帰係数が6.0と正(プラス)の値なので、塩分摂取量が多いと収縮期血圧が6.0 mmHg高いという関係にあり、これは負の相関関係ではなく、正の相関関係である
b.1日の塩分摂取量が1グラム多いと収縮期血圧は平均して6 mmHg高い。
→正しい
c.収縮期血圧と塩分摂取量には正の相関関係がある。
→正しい
d.収縮期血圧が1 mmHg高いと1日あたりの塩分摂取量は平均して6グラム多い。
→誤り: 収縮期血圧を目的変数、塩分摂取量を説明変数とした回帰分析なので、回帰係数の値は塩分摂取量が1 g多い場合に血圧が何 mmHg高くなるかを表している
e.1日あたりの塩分摂取量が1グラム多いと収縮期血圧は平均して75 mmHg高い
→誤り: 75は切片で塩分摂取量が0のときの血圧の平均を表している
設問 11-1-2
この回帰式の決定係数は以下のうちどれか。
決定係数(R²)
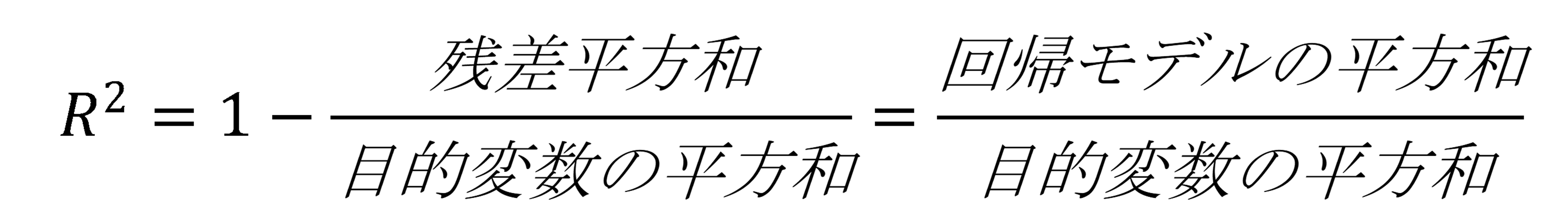
平方和: ある値を二乗して合計したもの
・残差平方和:残差を二乗して合計したもの
・目的変数の平方和: 目的変数の値と目的変数の平均値の差を二乗して合計したもの
・回帰モデルの平方和: モデルによる予測値と予測値の平均値の差を二乗して合計したもの
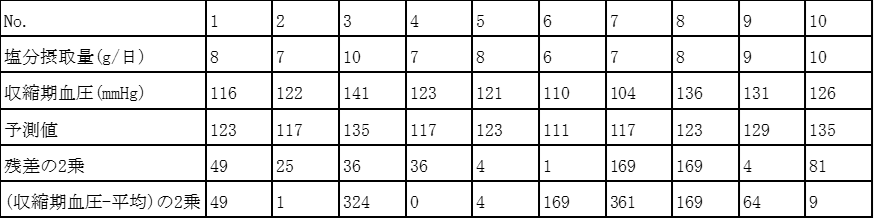
決定係数の計算手順は以下の通り。
1. 収縮期血圧を目的変数、塩分摂取量を説明変数とした回帰モデルは以下の通り
収縮期血圧=75.0+6.0×塩分摂取量+誤差
2. 目的変数(収縮期血圧)の平均=(116+122+…131+126)/10=123
3. 目的変数(収縮期血圧)の平方和=(各人の血圧ー血圧の平均)の2乗の合計
=(116-123)²+(122-123)² +…+ (131-123)² +(131-123)²=1150
4. 残差平方和=(各人の血圧ー回帰モデルによる予測値)の2乗の合計
=(116-123)²+(122-117)² +…+ (136-123)² +(131-129)²=574
5. 決定係数=1ー(残差平方和÷目的変数の平方和)
=1ー574÷1150=0.500869…≒0.501
設問 11-2-1
重回帰分析で仮定していないのはどれか。
重回帰分析で仮定しているのは、誤差の正規性、等分散性、独立性。
したがって、「誤差の一致性」が正解