はじめに
コーヒーが心血管イベントに有害なのではないかとの仮説を研究した、La Vecchiaの文献1のデータをもとに、Case Crossover Designの手法を紹介したこちらの文献2のスクリプトをまとめてみました。手法を試す例題として選んだオリジナルの文献1の結論は必ずしも広く受け入れられているものではないようです。
Case Crossover Designとは
製薬工業協会のタスクが作成した資料だと次のように説明されています。

「曝露がイベントの発生に及ぼす影響が投薬後の一定の期間に限定され,…と仮定できる状況で適応される」としています。集計上、一定期間とそれ以外の期間を比較していますので「投薬後の一定期間にことさら高い発現率(強い影響)があるかどうかを検定している」のではないかと言う気もします。
Modern Epidemiology by Rothmanでも次のように説明していて、一定の仮定の上での、caseとcontrolの比較という立場のようです。
When the exposure under study is defined by proximity to an environmental source (e.g., a power line), it may be possible to construct a specular (hypothetical) control for each case by conducting a “thought experiment.” Either the case or the exposure source is imaginarily moved to another
location that would be equally likely were there no exposure effect; the case exposure level under this hypothetical configuration is then treated as the (matched) “control” exposure for the case (Zaffanella et al., 1998). When the specular control arises by examining the exposure experience of the case outside of the time in which exposure could be related to disease occurrence, the result is called a case-crossover study.
Case Crossover Design のRコード
とりあえずコード部分はこのようになります。
##################################
#
# Case Crossover design converted from
# Ann Transl Med 2016;4(18):341
#
# Example from
# La Vecchia and colleagues
# coffee intake and MI
# Am J Epidemiol 1989;130:481-5
#
# 12/2/2017 Y. Oshima
#
##################################t<-c(9,1/3,3,22,6,7,12,5,0.5,24)
frq<-c(730,365,36,1820,2920,24,730,730,3650,365)T<-365*24
efftime<-ifelse(t>=1,0,1)
rr<-sum(efftime*(T-frq))/sum((1-efftime)*frq)
rrvar.log<-sum(frq*(T-frq))/(sum(efftime*(T-frq))*sum((1-efftime)*frq))
se.log<-sqrt(var.log)
lo.log<-log(rr)-1.96*se.log
hi.log<-log(rr)+1.96*se.log
lo<-exp(lo.log)
hi<-exp(hi.log)or<-sum(efftime*(T-frq-(1-efftime)))/sum((1-efftime)*(frq-efftime))
var.log.or<-(sum(efftime*(T-frq-1+efftime)*(efftime+ T-frq-1+efftime))/(2*(sum(efftime*(T-frq-1+efftime)))^2))+(sum(efftime*(T-frq-1+efftime)*(1-efftime+frq-efftime)+(1-efftime)*(frq-efftime)*(efftime+(T-frq-1+efftime)))/(2*sum(efftime*(T-frq-1+efftime))*sum((1-efftime)*(frq-efftime))))+(sum((1-efftime)*(frq-efftime)*(1-efftime+frq-efftime))/(2*(sum((1-efftime)*(frq-efftime)))^2))
se.log.or<-sqrt(var.log.or)
lo.log.or<-log(or)-1.96*se.log.or
hi.log.or<-log(or)+1.96*se.log.or
lo.or<-exp(lo.log.or)
hi.or<-exp(hi.log.or)matrix<-matrix(round(c(rr,lo,hi,or,lo.or,hi.or),2),nrow=2,byrow=TRUE)
rownames(matrix)<-c(“RR”,”OR”)
colnames(matrix)<-c(“Value”,”low 95% CI”,”high 95% CI”)
matrixmat<-matrix(, nrow = T-1, ncol = 0)
for (i in 1:10) {
if (T%%frq[i]==0) {
exposure<-c(rep(c(1,rep(0,T/frq[i]-1)),frq[i]))[-T]
} else {
exposure<-c(rep(c(1,rep(0,trunc(T/frq[i])-
1)),frq[i]),rep(0,T-frq[i]*trunc(T/frq[i])))[-T]
}
mat<-cbind(mat,exposure)
}commat<-rbind(efftime,mat)
library(reshape2)
data.wide<-as.data.frame(commat)
colnames(data.wide)<-c(1:10)
data<-melt(data.wide,measure=c(1:10))
colnames(data)<-c(“id”,”exposure”)
data$case<-rep(c(1,rep(0,T-1)),5)
head(data)library(survival)
mod<- clogit(case~exposure+strata(id),data)
summary(mod)data$clock<-c(rep(1,T/(365*4)),rep(2,T/(365*4)),rep(3,T/(365*4)),rep(4,T/(365*4)))
mod.adj<- clogit(case~exposure+clock+strata(id),data)
summary(mod.adj)
結果の照合
Cochran-Mantel-Haenszelのオッズ比
論文では次の通り

スクリプトを走らせると、一致しています。
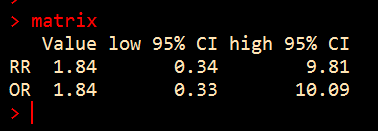
Conditional logistic regressionのオッズ比
論文では

スクリプトを走らせると、こちらも一致しています。(当たり前か?)

