はじめに
手持ちの単変量の分布を確率密度関数に当てはめて母数を推定する(よくわからない)
使うデータは他のページで作成したdf.testDATA
スクリプト
library(fitdistrplus) # 分布のテスト x <- df.testDATA$Time2Onset y <- max(df.testDATA$Time2Onset) min(df.testDATA$Time2Onset) ################ distribution test ################ normmlefit <- fitdist(x, "norm", "mle"); fit <- normmlefit; gofstat(fit); plot(fit) lnormmlefit <- fitdist(x + 0.1, "lnorm", "mle"); fit <- lnormmlefit; gofstat(fit); plot(fit) poismlefit <- fitdist(x, "pois", "mle"); fit <- poismlefit; gofstat(fit); plot(fit) expmlefit <- fitdist(x, "exp", "mle"); fit <- expmlefit; gofstat(fit); plot(fit) gammammefit <- fitdist(x, "gamma", "mme"); fit <- gammamlefit; gofstat(fit); plot(fit) nbinommlefit <- fitdist(x, "nbinom", "mle"); fit <- nbinommlefit; gofstat(fit); plot(fit) geommlefit <- fitdist(x, "geom", "mle"); fit <- geommlefit; gofstat(fit); plot(fit) betammefit <- fitdist(x/y, "beta", "mme"); fit <- betamlefit; gofstat(fit); plot(fit) unifmlefit <- fitdist(x, "unif", "mle"); fit <- unifmlefit; gofstat(fit); plot(fit) logismlefit <- fitdist(x, "logis", "mle"); fit <- logismlefit; gofstat(fit); plot(fit)
結果
よくフィットしてそうなのはbetaかgammaの様です
ロジスティック分布
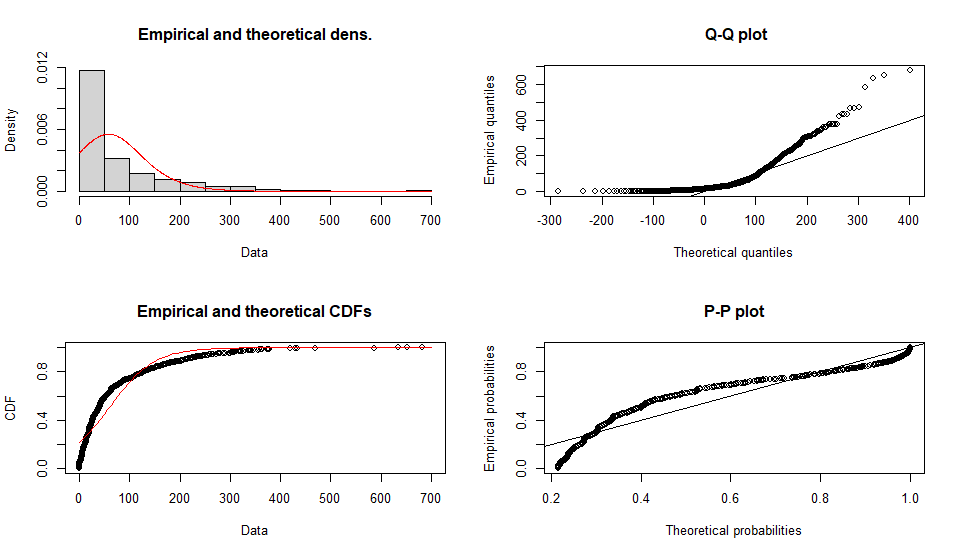
Fitting of the distribution ' logis ' by maximum likelihood
Parameters :
estimate Std. Error
location 58.31789 2.418478
scale 45.17608 1.249104
Loglikelihood: -5863.559 AIC: 11731.12 BIC: 11740.93
Correlation matrix:
location scale
location 1.0000000 0.1570439
scale 0.1570439 1.0000000
一様の分布(定数)
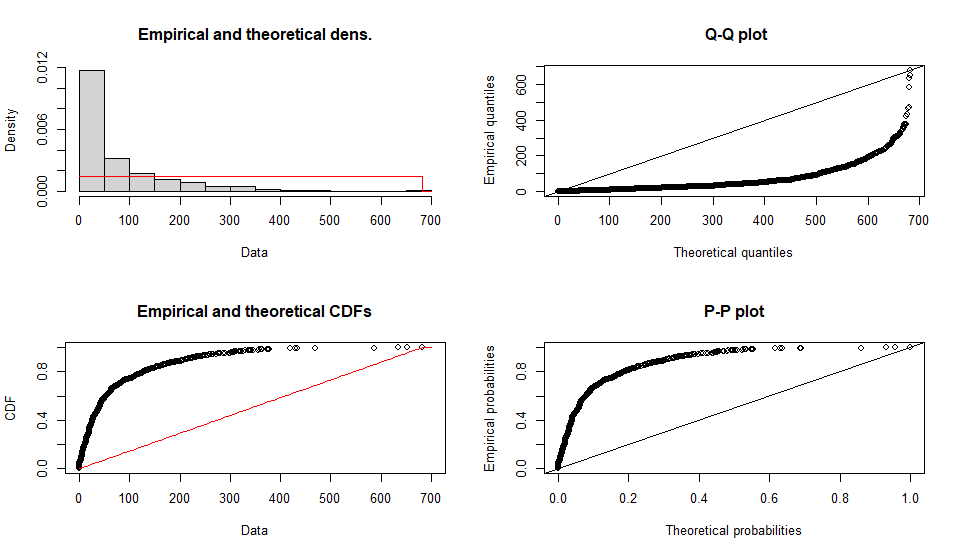
Fitting of the distribution ' unif ' by maximum likelihood
Parameters :
estimate Std. Error
min 0 NA
max 682 NA
Loglikelihood: -6525.03 AIC: 13054.06 BIC: 13063.87
Correlation matrix:
[1] NA
beta分布
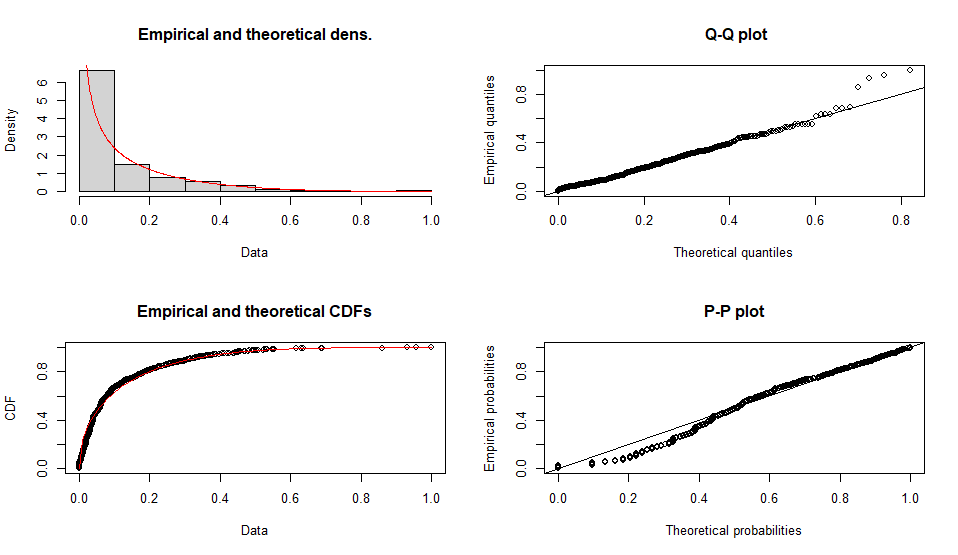
Fitting of the distribution ' beta ' by matching moments
Parameters :
estimate
shape1 0.4604008
shape2 3.6574364
Loglikelihood: NaN AIC: NaN BIC: NaN
geom分布
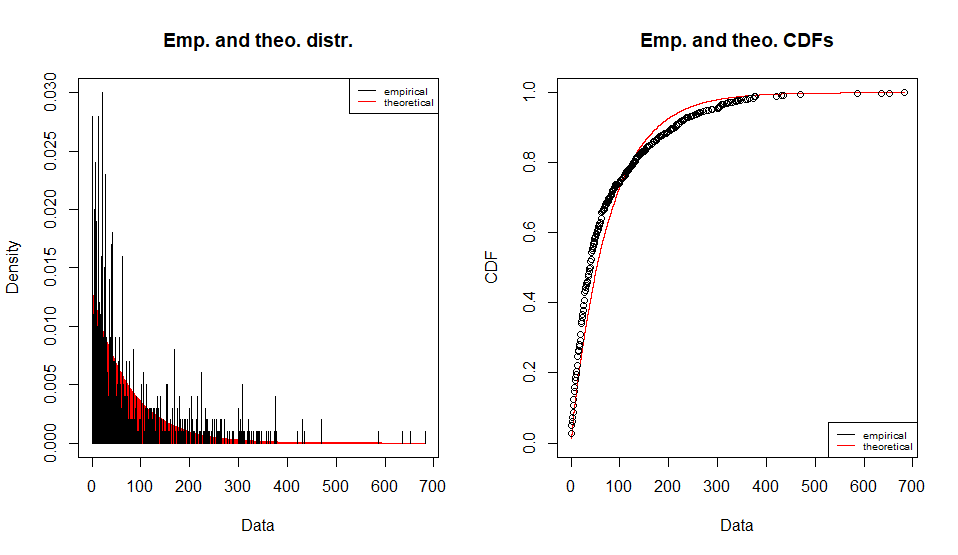
Fitting of the distribution ' geom ' by maximum likelihood
Parameters :
estimate Std. Error
prob 0.01294465 0.0004042749
Loglikelihood: -5340.572 AIC: 10683.14 BIC: 10688.05
負の二項分布
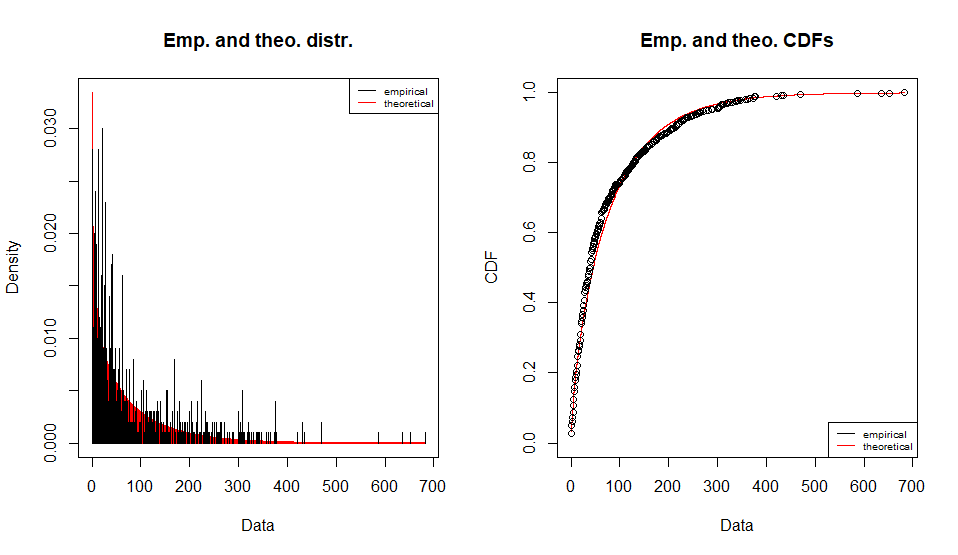
Fitting of the distribution ' nbinom ' by maximum likelihood
Parameters :
estimate Std. Error
size 0.7293184 0.02936535
mu 76.2394754 2.83607459
Loglikelihood: -5307.489 AIC: 10618.98 BIC: 10628.79
Correlation matrix:
size mu
size 1.0000000000 0.0001760878
mu 0.0001760878 1.0000000000
gamma分布
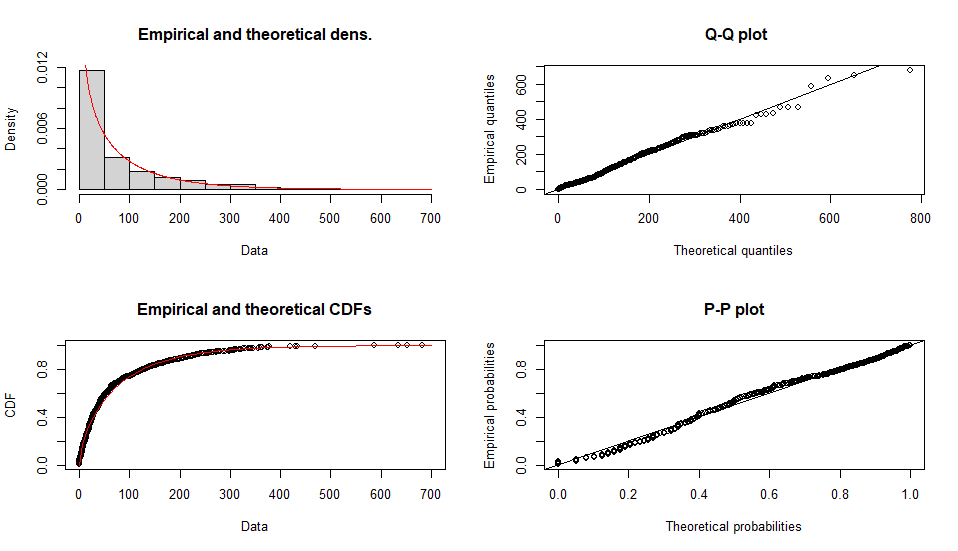
Fitting of the distribution ' gamma ' by matching moments
Parameters :
estimate
shape 0.644237078
rate 0.008448789
Loglikelihood: Inf AIC: -Inf BIC: -Inf
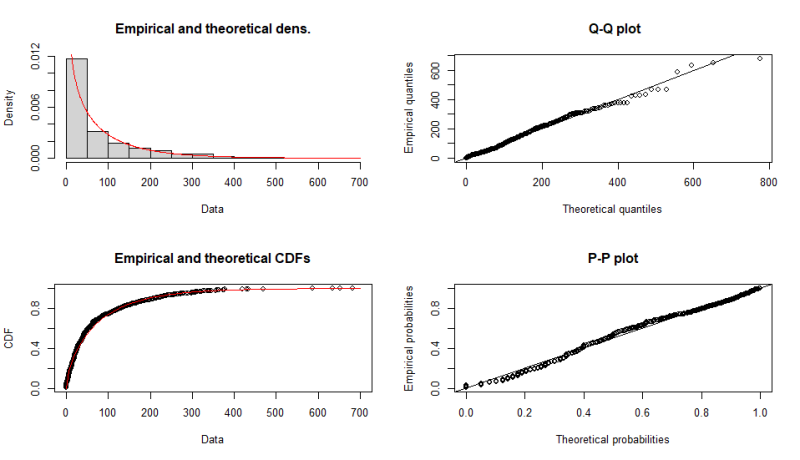
指数分布
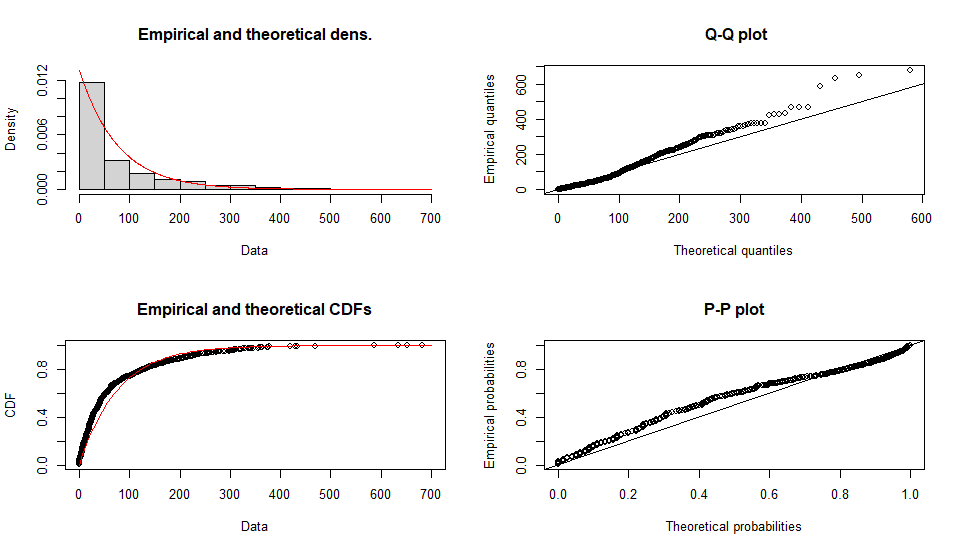
Fitting of the distribution ' exp ' by maximum likelihood
Parameters :
estimate Std. Error
rate 0.01311441 0.0004122862
Loglikelihood: -5334.044 AIC: 10670.09 BIC: 10675
ポワソン分布
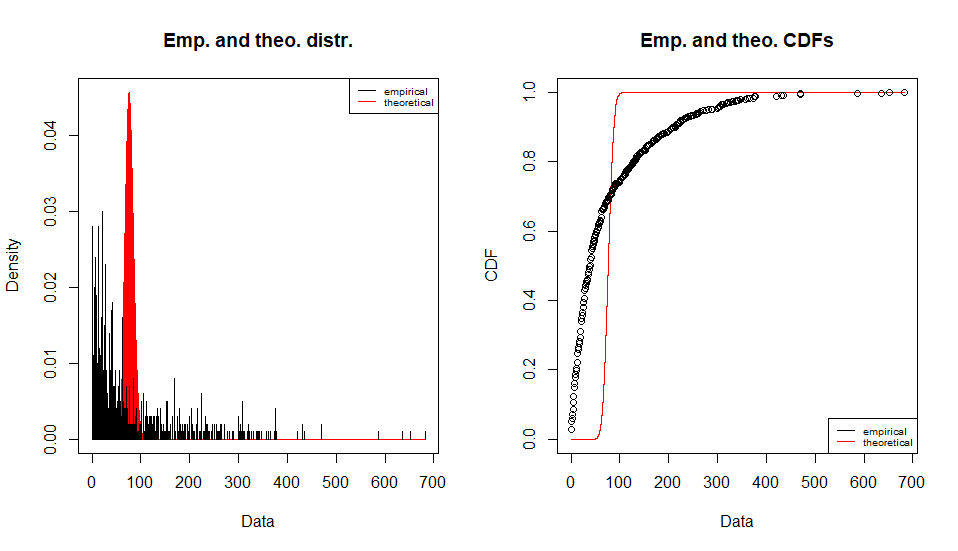
Fitting of the distribution ' pois ' by maximum likelihood
Parameters :
estimate Std. Error
lambda 76.252 0.2761377
Loglikelihood: -48448.44 AIC: 96898.87 BIC: 96903.78
対数正規分布
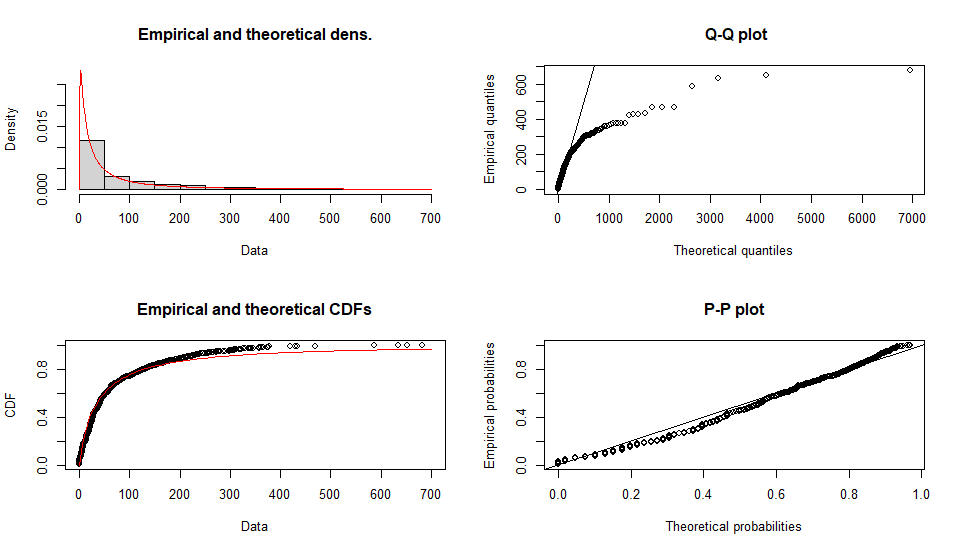
Fitting of the distribution ' lnorm ' by maximum likelihood
Parameters :
estimate Std. Error
meanlog 3.477753 0.05160282
sdlog 1.631824 0.03648864
Loglikelihood: -5386.39 AIC: 10776.78 BIC: 10786.6
Correlation matrix:
meanlog sdlog
meanlog 1 0
sdlog 0 1
正規分布
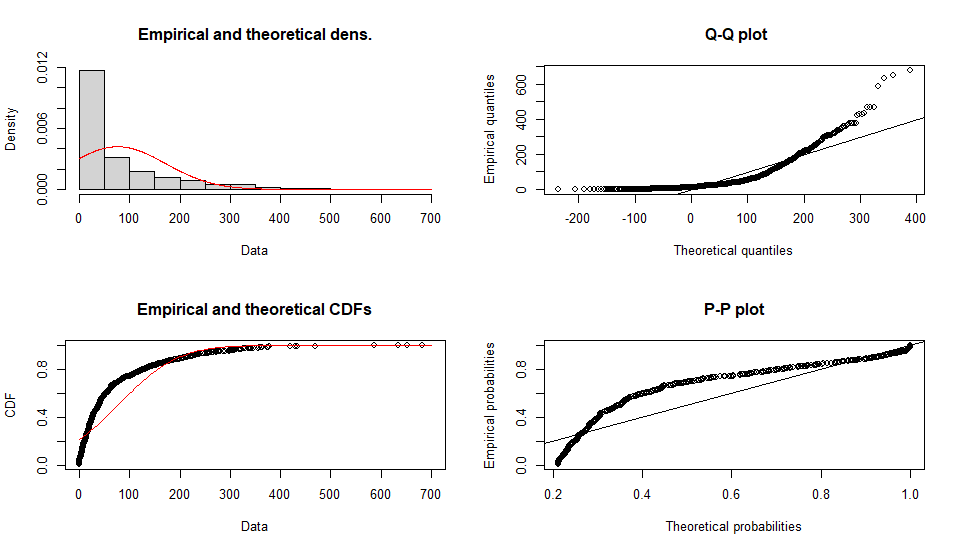
Fitting of the distribution ' norm ' by maximum likelihood
Parameters :
estimate Std. Error
mean 76.25200 3.004195
sd 95.00104 2.124288
Loglikelihood: -5972.826 AIC: 11949.65 BIC: 11959.47
Correlation matrix:
mean sd
mean 1 0
sd 0 1