Case Crossover Design – (2)
Relative Riskの計算の流れ
前回のコードを少し詳しく見てゆきます。
コーヒーの一時的な効果は、飲んでから1時間継続すると仮定します。Vector c には、AMIで救急外来を受診した患者さんから聞き取った、コーヒーを飲んでからAMI発症までの時間(hr)を代入します。
- t<-c(9,1/3,3,22,6,7,12,5,0.5,24)
1年間に何杯のコーヒーを飲むかという頻度(杯/year)をfrqに代入します。今回のこの値の使い方に基づき、一般化してこのスクリプトを使用する上では、1年あたりのTransient effect time(hr)がfrqという見方の方が良いだろうと思います。
- frq<-c(730,365,36,1820,2920,24,730,730,3650,365)
Tには、1年間は何時間かという値を入れます。今回は全症例1年を観察期間にしたので定数になっていますが、一般化する上では、評価の対象にした観察期間と理解すると良いだろうと思います。症例ごとに観察期間が違う場合はTもベクターにできると思います。
- T<-365*24
efftimeには、AMIの発症がコーヒーを飲んで1時間以上経過していたらfalse (0), 1時間未満であればtrue(1)というフラグを代入します。Transient effect timeを1hrにしていますので、判定の条件は t>=1を使用していますが、Transient effect timeが2hrなら判定条件をt>=2にしたらよいでしょう。その際もフラグ(返り値)は 0, 1のままで結構です。
- efftime<-ifelse(t>=1,0,1)
RRの計算
Mantel-Haenszelの計算式からRR (relative risk) を計算します

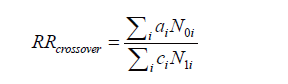
としましたので、次の式になります。
- rr<-sum(efftime*(T-frq))/sum((1-efftime)*frq)
分散を求める式では
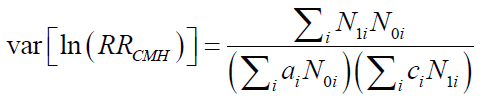
この部分をコード化すると
- var.log<-sum(frq*(T-frq))/(sum(efftime*(T-frq))*sum((1-efftime)*frq))
標準誤差は分散の平方根で以下のようになります
- se.log<-sqrt(var.log)
- lo.log<-log(rr)-1.96*se.log
- hi.log<-log(rr)+1.96*se.log
- lo<-exp(lo.log)
- hi<-exp(hi.log)
ORの計算
オッズ比は次の式で表現されますので
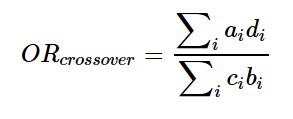
これをコード化すると
- or<-sum(efftime*(T-frq-(1-efftime)))/sum((1-efftime)*(frq-efftime))
分散は次のように表現されますので(元論文のこの式の「=」の左側、var[ln(RRchm)] は、おそらくvar[ln(ORchm)]の誤植だろうと思っています)
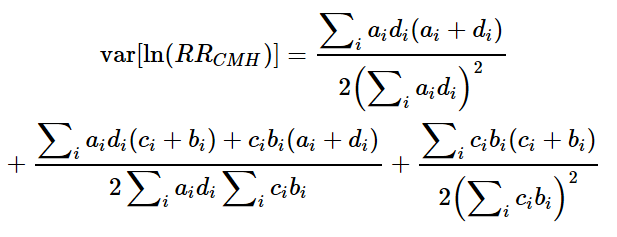
これをコード化すると次のようになります
- var.log.or<-(sum(efftime*(T-frq-1+efftime)*(efftime+ T-frq-1+efftime))/(2*(sum(efftime*(T-frq-1+efftime)))^2))+(sum(efftime*(T-frq-1+efftime)*(1-efftime+frq-efftime)+(1-efftime)*(frq-efftime)*(efftime+(T-frq-1+efftime)))/(2*sum(efftime*(T-frq-1+efftime))*sum((1-efftime)*(frq-efftime))))+(sum((1-efftime)*(frq-efftime)*(1-efftime+frq-efftime))/(2*(sum((1-efftime)*(frq-efftime)))^2))
標準誤差は分散の平方根で以下のようになります
- se.log.or<-sqrt(var.log.or)
- lo.log.or<-log(or)-1.96*se.log.or
- hi.log.or<-log(or)+1.96*se.log.or
- lo.or<-exp(lo.log.or)
- hi.or<-exp(hi.log.or)
で、集計にはこれとは別のアプローチが紹介されていましたので次の記事へつづきます
