Rでサンプルサイズあるいはパワーを計算

はじめに

臨床研究をするためのプロトコールに書くような、厳密性のある見積もりは統計の専門家に相談して進める必要があるのですが、専門家に依頼するとそれなりに前提を整理してお膳立てしてからお願いすることになります。また、専門家にきちんと検討してもらうには時間も必要です。しかしそこに至る前の段階で、段取りを組み立てて行くために、厳密性を犠牲にして大まかな見積もりが欲しいという場面も少なからずあります。（細かい前提をすっ飛ばすので雑です、すみません）

コードです

setwd("c://Documents/R/hogehoge/")
library(pwr)

#  i) コントロール群で50%, 実薬群で25%　（と薬効やイベントを想定）
#  検出力 power は80%, p=0.005 (これは意図的に汎用されているP=0.05や0.01より小さくしました）
out_i <- pwr.2p.test(h = ES.h(p1 = 0.50, p2 = 0.25),
           sig.level = 0.005,
           power = 0.80,
           alternative = "two.sided")
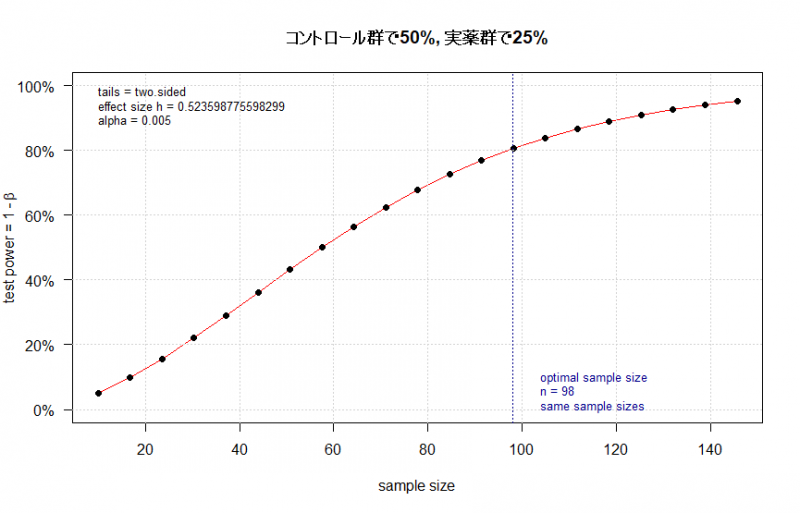
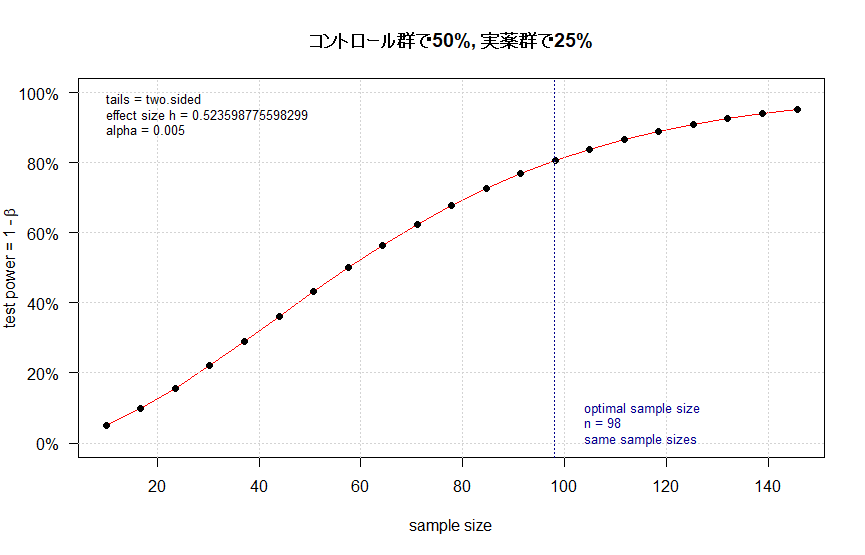
plot(out_i, main = "コントロール群で50%, 実薬群で25%")

# ii) コントロール群で50%, 実薬群で 40% 　(同上)
# 検出力 power は80%, p=0.005 (これは意図的に汎用されているP=0.05や0.01より小さくしました） 
out_ii <- pwr.2p.test(h = ES.h(p1 = 0.50, p2 = 0.40),
                    sig.level = 0.005,
                    power = 0.80,
                    alternative = "two.sided")
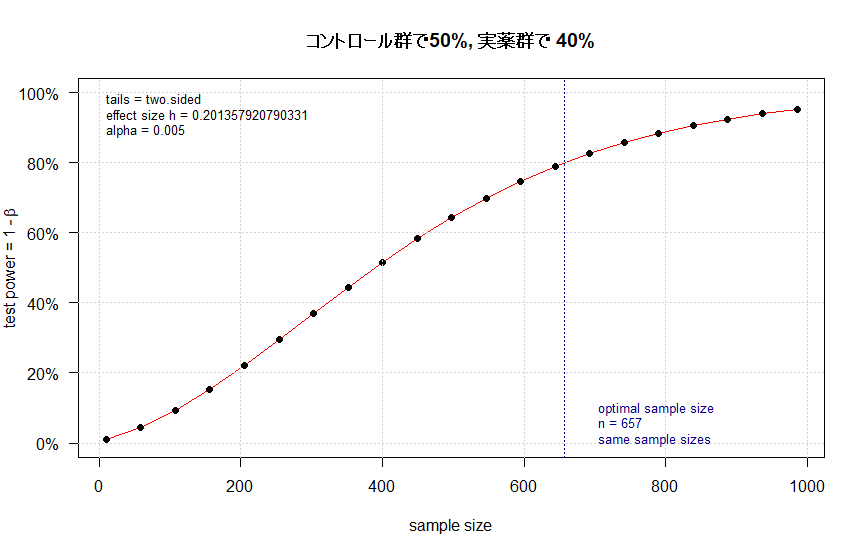
plot(out_ii, main = "コントロール群で50%, 実薬群で 40%")

 

結果です

i) コントロール群で50%, 実薬群で25%　（と薬効やイベントを想定）, 検出力 power は80%, p=0.005 (これは意図的に汎用されているP=0.05や0.01より小さくしました）

pwrライブラリーを使わずに、組み込み関数を用いると、図は出ませんが次のようになります。

power.prop.test(p1=0.50, p2=0.25, sig.level = 0.005, power = 0.80)

結果です

     Two-sample comparison of proportions power calculation 

              n = 98.28936
             p1 = 0.5
             p2 = 0.25
      sig.level = 0.005
          power = 0.8
    alternative = two.sided

NOTE: n is number in *each* group

図中に示されたn=98とだいたい一致しました。

ii) コントロール群で50%, 実薬群で 40% 　(同上)

pwrライブラリーを使わずに、組み込み関数を用いると、図は出ませんが次のようになります。

power.prop.test(p1=0.50, p2=0.40, sig.level = 0.005, power = 0.80)

この結果です

     Two-sample comparison of proportions power calculation 

              n = 657.4394
             p1 = 0.5
             p2 = 0.4
      sig.level = 0.005
          power = 0.8
    alternative = two.sided

NOTE: n is number in *each* group

こちらも図中の657とだいたい一致しました。