SAHのアウトカム予測モデルの構築

pROCパッケージのaSAHデータを使用して、多変量ロジスティック解析を行い、outcomeを他の変数で予測する予測式を作成してみましょう。

以下は具体的な手順です：

必要なパッケージのインストールと読み込み
データの読み込み
多変量ロジスティック回帰モデルの構築
モデルの結果を解釈する

ステップ1: パッケージのインストールと読み込み

まず、必要なパッケージをインストールして読み込みます。

install.packages("pROC")
install.packages("dplyr")

library(pROC)
library(dplyr)
library(ggplot2)

ステップ2: データの読み込み

次に、aSAHデータを読み込みます。予測式を作成する際にはカテゴリーを1, 0 の数字に置き換えたほうがいいので、outcome, gender wfnsをダミー変数に変換します。wfinsは各値を別々のダミー変数wfns2, wfns3, wfns4, wfns5に置き換えました。これらすべてが0ならwfns1が1になるはず（欠測値が無い）という事で、wfns1は作成しませんでした。

data(aSAH, package = "pROC")

# outcome変数を数値型のダミー変数に変換
aSAH <- aSAH %>%
  mutate(good_outcome = ifelse(outcome == "Good", 1, 0))

# gender変数を数値型のダミー変数に変換
aSAH <- aSAH %>%
  mutate(gender_numeric = ifelse(gender == "Male", 1, 0))

# wfns変数のダミー変数を作成し、データフレームに追加
aSAH <- aSAH %>%
  mutate(wfns2 = ifelse(wfns == 2, 1, 0),
         wfns3 = ifelse(wfns == 3, 1, 0),
         wfns4 = ifelse(wfns == 4, 1, 0),
         wfns5 = ifelse(wfns == 5, 1, 0))

ステップ3: 多変量ロジスティック回帰モデルの構築

多変量ロジスティック回帰モデルを作成します。この例では、outcomeを他の変数で予測するモデルを構築します。

# ロジスティック回帰モデルの構築
model <- glm(good_outcome ~ gender_numeric + age + wfns2 + wfns3 + wfns4 + wfns5 + s100b + ndka, 
             data = aSAH, family = binomial)

# モデルの概要を表示 係数coefを抽出
summary(model)
summary_model <- summary(model)
coef_model <- summary_model$coefficients

# モデル
logit_P = coef_model[1] + coef_model[2]*aSAH$gender_numeric + coef_model[3]*aSAH$age +
 coef_model[4]*aSAH$wfns2 + coef_model[5]*aSAH$wfns3 + coef_model[6]*aSAH$wfns4 +
 coef_model[7]*aSAH$wfns5 + coef_model[8]*aSAH$s100b + coef_model[9]*aSAH$ndka

aSAH$logit_P <- logit_P

ステップ4: モデルの結果や予測式の性能を見てみよう

ステップ３までで、モデルに基づいて予測式を作成しました。

# 散布図の作成 データの外観を確認する
ggplot(aSAH, aes(x=outcome, y=logit_P, color=outcome)) +
  geom_point() +
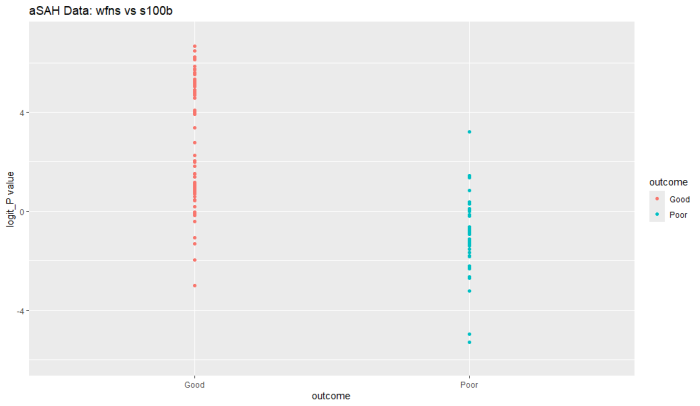
  labs(title="aSAH Data: wfns vs s100b",
       x="outcome",
       y="logit_P value") + 
  scale_y_continuous(limits = c(-6, 7))

# とりあえずROCカーブを描いてみよう
# roc1 <- aSAH %>% roc(outcome, logit_P)
# ggroc(roc1)

# 散布図の作成 データの外観を確認する
ggplot(aSAH, aes(x=outcome, y=logit_P, color=outcome)) +
  geom_point() +
  labs(title="aSAH Data: outcome vs logit_P",
       x="outcome",
       y="logit_P value")+
  scale_y_continuous(limits = c(-6, 7))

# ROC曲線の作成　s100b血清値でSAHの予後予測する設定
roc_obj <- roc(aSAH$outcome, aSAH$logit_P)

# ROC曲線のプロット
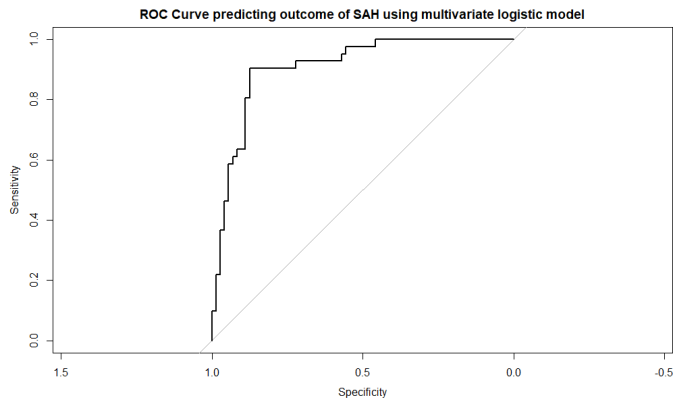
plot(roc_obj, main="ROC Curve predicting outcome of SAH using multivariate logistic model")

# AUCの計算
auc_value <- auc(roc_obj)
print(paste("AUC:", auc_value))

# 感度、特異度、陽性的中率、陰性的中率を計算
coords_obj <- coords(roc_obj, x="best", ret=c("sensitivity", "specificity", "ppv", "npv"))

# 結果を出力
print(paste("感度:", coords_obj["sensitivity"]))
print(paste("特異度:", coords_obj["specificity"]))
print(paste("陽性的中率:", coords_obj["ppv"]))
print(paste("陰性的中率:", coords_obj["npv"]))

# 尤度比を算出、その前に改めて感度と特異度を取得
coords_obj <- coords(roc_obj, x="best", ret=c("sensitivity", "specificity"))
sensitivity <- coords_obj["sensitivity"]
specificity <- coords_obj["specificity"]

# 陽性尤度比 (LR+) と 陰性尤度比 (LR-) を計算
positive_likelihood_ratio <- sensitivity / (1 - specificity)
negative_likelihood_ratio <- (1 - sensitivity) / specificity

# 結果を出力
print(paste("陽性尤度比 (LR+):", positive_likelihood_ratio))
print(paste("陰性尤度比 (LR-):", negative_likelihood_ratio))

# 最適な閾値を取得
best_coords <- coords(roc_obj, x = "best", ret = c("threshold", "sensitivity", "specificity"))

# 最適な閾値を表示
best_coords

データの散布図、教科書のロジスティック回帰のlogitの説明で見たことあるような雰囲気