相関
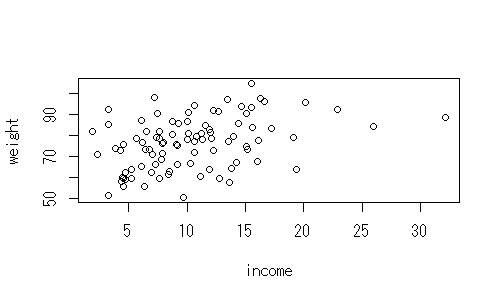
2つの連続変数同士の相関は、cor.test()関数を用いて調べることができます。
cor.test(1つめの連続変数, 2つめの連続変数, method = "pearsonもしくは指定なしか、spearman、kendall")
身長と体重に相関関係が見られるかどうかを検討するためのコードは下記の通りになります。最初に図示して、分布を確かめることはもちろん必須です。
## 相関の検定(身長と体重)
2つの変数間に相関関係があるか確かめる場合に行う。
```{r cortest}
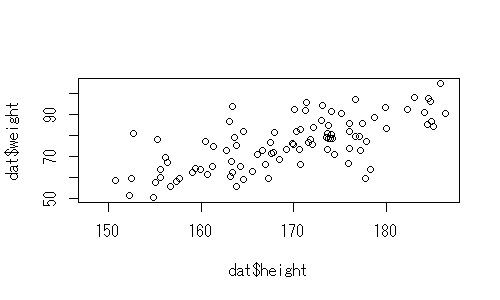
plot(dat$height, dat$weight)
cor.test(dat$height, dat$weight)
```
> cor.test(dat$height, dat$weight)
Pearson's product-moment correlation
data: dat$height and dat$weight
t = 9.3422, df = 93, p-value = 5.041e-15
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.5748646 0.7869766
sample estimates:
cor
0.6957931
結果から、身長と体重の間には、有意な相関関係があり、相関係数は0.70であることがわかります。また、このとき、相関係数の95%信頼区間は、[0.57, 0.79]となります。
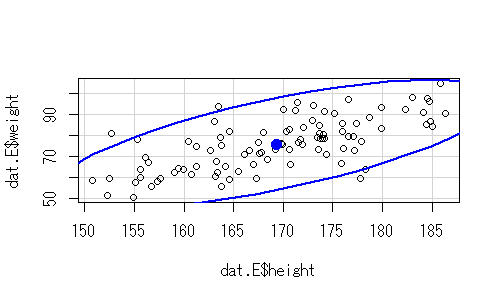
相関関係をみる場合、集中楕円を描くことがある。利用する関数はdataEllipse()関数で、carパッケージに入っている。
## 集中楕円の描画
集中楕円は、欠損値があると描画されないので、最初にサブセットを作成してから実行します。
```{r corell}
library("car")
dat.E = dat[, c("height", "weight")]
dat.E = subset(dat.E, complete.cases(dat.E))
dataEllipse(dat.E$height, dat.E$weight, levels = 0.95)
```