2つの平均の比較
Rでは2変量の平均値の差の検定にウェルチのt検定を使うことがデフォルトになっています。また、事前に等分散が仮定できる状態でなければ、いちいちF検定をせず、そのままウェルチのt検定を行った方がよいことがシミュレーションなどで示されています( t検定(分散が等しいかどうか不明の場合))。使い方は下記の通りです。
t.test(比較したい変数 ~ 2群に分ける変数, data = データフレーム名)
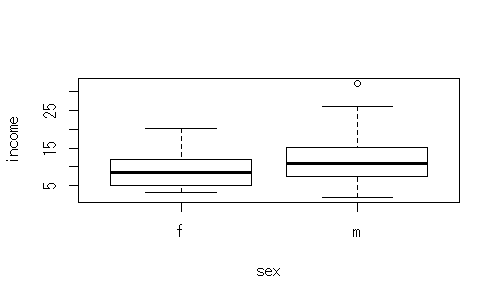
男女間で体重の差があるかどうかを検討するためのコードは下記の通りとなります。最初に図示して、分布を確かめることは必須です(もちろん、ヒストグラムを確認してもかまいません)。
## 平均値の差の検定
平均値の差の検定には、t.test()関数を使います。
```{r ttest}
plot(weight ~ sex, data = dat)
t.test(weight ~ sex, data = dat)
t.test(dat$weight[dat$sex == "m"], dat$weight[dat$sex == "f"])
```

> t.test(weight ~ sex, data = dat)
Welch Two Sample t-test
data: weight by sex
t = -2.4155, df = 92.99, p-value = 0.01767
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-10.737885 -1.048313
sample estimates:
mean in group f mean in group m
72.9546 78.8477
結果から、fグループの平均は、73.0、mグループの平均は78.8で、有意に体重に差があることがわかります。また、このとき、両者の差の95%信頼区間は、[-10.74, -1.05]となります。
t.test()関数において、2つのベクトルを並列に並べるt.test(dat$weight[dat$sex == "m"], dat$weight[dat$sex == "f"])の書き方も問題ありませんが、t.test(weight ~ sex, data = dat)の方が、性別ごとに体重の差を調べたということがわかりやすいのでおすすめです。
等分散が仮定できる場合、オプションとしてt.test()関数の引数に、「var.equal = TRUE」を追加します。例:t.test(A, B, var.equal = TRUE)
対応のあるt検定
比較対象の2つのデータが対応している場合、「paired = TRUE」というオプションを引数に指定し、対応のあるt検定を行います。対応のあるt検定では、対応の前後関係を示す変数よりも、2つの変数自体の比較が多くなる可能性が高いと思いますので、モデル式を用いたt検定の使い方よりも、変数を2つ並べた使い方の方がよく使われるかもしれません。
t.test(ある変数1, ある変数と対応がある変数2, paired = TRUE)
t.test(比較したい変数 ~ 対応関係を示す変数, paired = TRUE, data = データフレーム名)
用意したデータに対応のある変数がないので、実際に対応があるつもりの変数を作成してみて、実験してみましょう。このように、簡単に疑似データを作って試してみることができるのもRの強みの一つです。
## 対応のあるt検定
比較対象の2つのデータが対応している場合、「paired = TRUE」というオプションを引数に指定し、対応のあるt検定を行います。
```{r ttestpair}
set.seed(1)
a1 = rnorm(50, 60, 10)
a2 = rnorm(50, 55, 12)
t.test(a1, a2, paired = TRUE)
t.test(a1 - a2, mu = 0)
```
> set.seed(1)
> a1 = rnorm(50, 60, 10)
> a2 = rnorm(50, 55, 12)
> t.test(a1, a2, paired = TRUE)
Paired t-test
data: a1 and a2
t = 2.2331, df = 49, p-value = 0.03014
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.4601578 8.7329729
sample estimates:
mean of the differences
4.596565
> t.test(a1 - a2, mu = 0)
One Sample t-test
data: a1 - a2
t = 2.2331, df = 49, p-value = 0.03014
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
0.4601578 8.7329729
sample estimates:
mean of x
4.596565
ちなみに、上記結果より、対応のあるt検定とは、2変量の差が0と等しいかどうかを調べる1標本のt検定と全く同じものであることがわかります。
set.seed()関数は、乱数を扱う際に種となる数字を指定して、意図的に同じ結果を再現するための関数で、rnorm()関数は、正規分布に従う乱数を生成する関数です。上のコードでは、seedを1に指定して、rnorm()関数を2回使って、a1に平均60、標準偏差10の乱数を50個、a2に平均55、標準偏差12の乱数を50個作成しています。この50個ずつが同じ人のダイエット前の体重と、ダイエット後の体重などと仮定して解析したものが上のコードになります。