統計学的画像再構成法である

OSEMアルゴリズムの基礎論

【第1章】確率・統計の基礎

１．９　ベルヌーイ分布

統計学を特に勉強したことのない方でも、正規分布（ガウス分布）は聞いたことがあるのではないでしょうか？でもベルヌーイ分布は聞いたことがない方も多いと思います。しかしこの分布はいたって簡単な分布なのです。コインには裏か表しかなく、コイントスでどちらが出るのかを当てようとするときを考えましょう。コインが立つとかを考えなければ、コインは裏か表しか出ません。このように、結果が２通りしか存在しないとき、この試行はベルヌーイ分布に従うといいます。コインでなくても、オセロの駒（白か黒）でももちろん同じです。それ以外にも、ある薬が患者に効いたか効かなかったかも同様に考えられます。放射線の話をするならば、検出器に光子が入ったか入らなかったかの結果ははやりベルヌーイ分布に従います。

ではベルヌーイ分布を数式に表してみましょう。コインの話が簡単なので例にすれば、裏が（表が）出る確率はもちろん、0.5ですね。そして裏が出る時を、x=0とし、表が出る時をx=1としましょう。確率は0.5ですので、p=0.5とすると、ベルヌーイ分布f_x(x)は次式のようになります。

結果は２通りしかないのですから、確率変数は、x=0、1の２通りしかないのです。従ってこれ以外の確率は0となり、つまり起こり得ない（コインが立つということはない）ということです。

薬の例で考えれば、ある降圧剤が効く確率は治研の結果0.673であったとすれば、f_x(x)は次式のようになります。

このとき，x=0は薬が効かないとき，x=1は薬が効くときの変数です．

またベルヌーイ試行の平均と分散はそれぞれ、p、p(1-p)となります。つまりたくさん薬を使って，聞いた結果の確率はパラメータであるpに近づくということです．

さて，これがいったい放射線となんの関係が？？

1つの検出器に，光子が入ったか入らなかったかのみを問うとき，その結果はこのベルヌーイ分布に従いましょう．光子が検出器に入るか入らないかの2つに1つだからですね．

ベルヌーイ分布は軽くこのくらいにして、次からはだんだん難しくなり、本格的になってきます。心して？進みましょう！！

【Coffee Break】

ところで，“分布”ってなんでしょう？　「成人男子の身長の分布は正規分布に従う」とか，「事象Xiはポアソン分布からのランダム標本とする」とかの表現がそれらしい本にはちょくちょく書いてあります．そもそも分布なんてものは人間が考え出したものなんですが，例えば身長を例にとって考えてみましょう．次々に成人を捕まえてきて身長を計測します．そしてグラフに書いてみます．横軸は身長のクラスとしまして，150 cm 〜 160 cmの間とかにします．そして縦軸はそのクラスにいる人数です．さてその結果を図にしますと，こんなになったとしましょう．

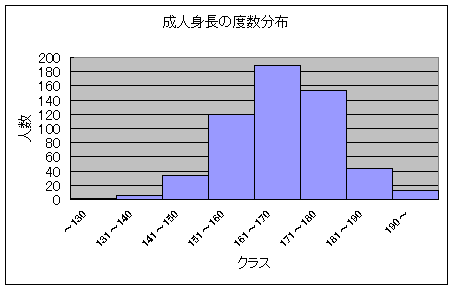
これを度数分布表といいます．この棒グラフの一番上の中心を滑らかな曲線で結んでみ見てください．富士山型になりませんか？　この身長の測定を無限回繰返すと（実際には出来ませんが）この曲線は左右対称の富士山型の末広がり曲線になります．これが後に出てくる“正規分布”なんですが，分布とは，こういった曲線の形状を関数であらわし，数学的な話をしやすくするための道具です．自然界の多くの現象の繰り返し頻度は，このような“分布”という形で示した関数にその頻度を近似して表せることを発見した多くの数学者がいます．（この項のベルヌーイやガウスなんかもその数学者たちの1人です)そして色々な現象を数学的に解明するのに，この分布という道具はなくてはならない存在になりました．無論放射線を扱うことに関連してもこの分布が深くかかわっています．