統計学的画像再構成法である
OSEMアルゴリズムの基礎論
【第1章】確率・統計の基礎
1.8 全確率の定理とベイズの定理
これからゆっくりですが、少し統計らしくなってきます。ここに解説する内容は、確率を考える上で、かつOSEMの理論を考える上で最も根本に係わる基礎概念です。とくにベイズの定理は、1.6で説明した条件付き確率に関係し、OSEMの概念を理解するのに大変重要な定理であります。ベイズ統計学という分野も確立しており、これだけで結構な厚さの本が多数あるくらいです。ここではあまり深く考えずに概要だけわかれば十分です。さて始めましょう。まずはこんな例を考えてみましょう。
《箱と黒玉を選ぶ》
全く同じ形の箱を2つ用意し、箱A1、箱A2とする。箱A1には黒玉が1個、赤玉が2個入っている。箱A2には黒玉が1個、赤玉が3個入っている。玉はみんな同じ大きさである。最初に箱A1、箱A2のどちらかの箱を選び、選んだ箱から玉を1つ取り出したとき、その玉が黒である確率はいくつだろうか?
箱A1を選び出す事象A1とし、その確率をP(A1)とする。また、箱A2を選び出す事象A2とし、その確率をP(A2)とする。さらに選び出された玉が黒玉である事象をBとし、その確率をP(B)とする。例を満たすことを記号で書くと2通り考えられよう。つまり、
A1∩B または A2∩B
の2通りである。両方の箱には黒玉があるので、箱A1と箱A2の両方をそれぞれに考えなくてはなりません。箱は2種類ですからどちらの箱が選ばれるかの確率は1/2です。箱A1には3個の玉がありそのうち1つが黒玉なので、黒玉が選ばれる確率は1/3です。また、箱A2には4個の玉がありそのうち1つが黒玉なので、黒玉が選ばれる確率は1/4です。従って、

これらよりP(B)をこれらの和ですから、
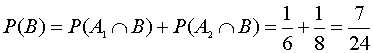
と計算されます。このような計算を以下のような図で書くとわかりやすいでしょう。
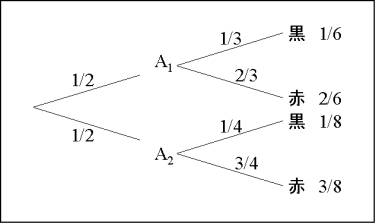
このような図を確率の樹(probability tree)と呼ぶことがあります。また各枝は、前の枝の事象が与えられたときの条件付き確率を表しています。
この例を一般的に書くと以下の定理がかけます。
【全確率の定理】(Total Probability Theorem)
A1、A2、・・・、Ai、・・・(i=1、2、・・・)を、標本空間全体を分割したものとする。
このときP(Ai) > 0ならば、事象Bに対して、
![]()
が成り立つ。
続いて、有名な“ポリヤの壺の問題”を紹介します。
***ポリヤの壺の問題***
壺の中にr個の赤い壺とb個の黒玉が入っている。玉は色以外は全く同じである。玉を1つ取り出しその色を見る。その取り出した玉とともに同色の玉をc個壺に戻す。これを繰り返し行ったとき、n回目に赤玉が出る事象をRn、黒玉が出る事象をBnとする。
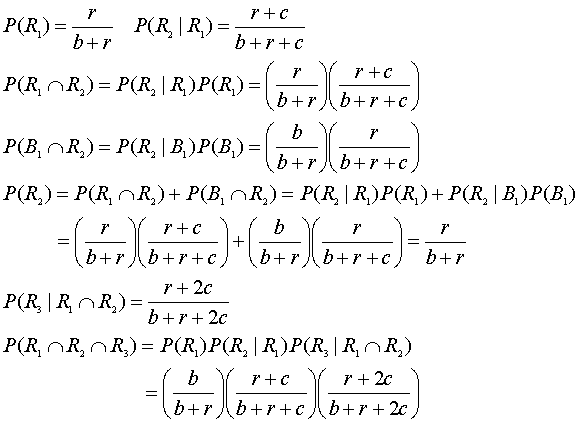
このように次々に事象Rnの同時確率が求められます。
さて、箱と黒玉を選ぶ例をもう一度考えてみましょう。今度は取り出されれた玉が黒であると知らされたとき(予言者がこう言ったとしてもいいが・・・)、選ばれた箱がA1である確率を考えてみる。
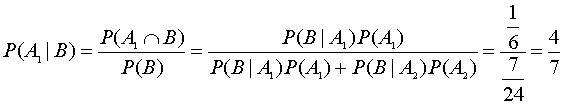
したがって、箱A1が選ばれる確率が、条件を与えられたことにより、1/2から4/7に変化したことになります。一般に次の超有名な定理が成り立ちます。
【ベイズの定理】(Bayes’ Theorem)
A1、A2、・・・、Ai、・・・(i=1、2、・・・)を、標本空間全体を分割したものとする。
このときP(Ai) > 0ならば、事象Bに対して、P(B)>0ならば、
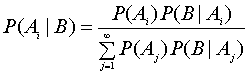
が成り立つ。
ここで、OSEMに関する言葉として、上記のP(Ai)を事前確率または先験確率(Prior Probability)、P(Ai|B)を事後確率(Posterior Probability)といいます。後者の事後確率は後のOSEMの本題で、重要な役目をします。
続いて、有名な“囚人のジレンマ”を紹介します。
***囚人のジレンマ***
3人の囚人A、B、Cは保釈になるチャンスは同じであるが、3人のうち1人だけが今回釈放になるという。つまり囚人Aが釈放される確率は1/3である。看守は3人のうち誰が釈放されるか知っているが保釈される本人にはいえない。いま、囚人Aが看守に他の2人のうちどちらが釈放されないか尋ねたところ、看守はBは釈放されないと答えた。この看守はうそはつかないとしたとき、囚人Aが釈放される確率は1/2になるのか??
以下のように記号の定義をして、ベイズの定理に従って計算してみる。
事象A:Aが釈放される 事象B:Bが釈放される 事象C:Cが釈放される
事象K:看守がBは釈放されないと答える
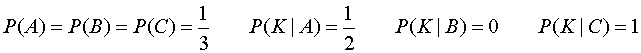
これを使って、
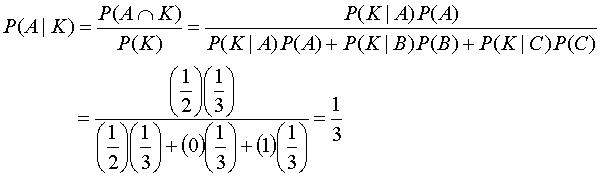
つまり、囚人Aにととっては気の毒だが、釈放される確率はやはり、1/3でした。残念!
次からは、確率関数と確率分布関数という概念と、分布の例を紹介し、本格的に統計学の世界に入り込んでいきましょう。