統計学的画像再構成法である

OSEMアルゴリズムの基礎論

【第1章】確率・統計の基礎

１．７ 自由度

　よくデータをコンピュータで解析すると、どこかにｎがいくつで、自由度がいくつでって出てないですか？　そして、なんだろう？と思いながら、どうやら標本数ｎから１引いた値なのだな！　と納得していませんか？　自由度という言葉は、言葉としては易しい言葉なので、きっと意味も易しいと思うかもしれません。でも実は結構わかりにくい内容であり、一言二言では納得できないと思います。一般的に一言で説明しろとすれば、“標本の性質を示す数”となるのですが、余計わかりませんよね。またいくつか例を上げながら説明していきましょう。

　（１．２）で標準偏差の計算にこの自由度が出てきました。ここでは、みなさんがよく使う“相関直線”と“普通の直線”を例にします。相関直線とはある標本の2つの変数に、直線関係がどの程度あるか？　を示すものです。このときこの直線は必ず2つのデータの、平均値の座標を通る性質があります。一方のデータの平均値を、他方の平均値をとすれば、必ず（、）を通るわけです。そこで図６を見てみましょう。

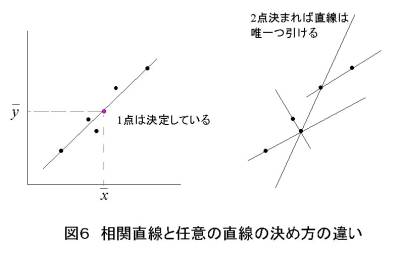
任意に2点を決めれば、その点を通る直線は唯一つ引くことができます。ところが、相関直線は必ず（、）を通るという条件付ですから、直線を引くための条件である任意の2点のうち1点はすでに決まっているわけです。これを自由度に当てはめると、直線の自由度は２で、相関直線の自由度は１といえます。

　今度は、（１．２）の最後に出てきた式を思い出しましょう。次の式です。

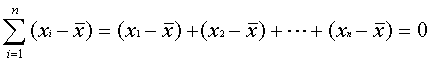
これを次のように変形します。

　　　　　　　

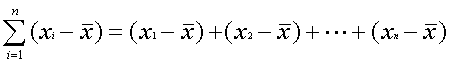
　移行すると、

この式の意味するところは、平均値がわかっていれば、x_nはx₁からx_n-1とで決まってしまいます。データを任意にn個取っているのでが、実は最後の１つは上記のような拘束があるのです。つまりn個のデータのうち任意なデータとはn-1個なのです。

　なにかパッとしれませか？ここではそれほど深く考えなくても大丈夫です。「ふ〜ん」って感じで結構です。ただデータにはかならずそれぞれに自由度が関係していると思っていてください。大抵は、データ数から平均値の個数を引いた値と思っていればいいと思います。そして、自由度は統計表（統計関係の本の巻末に必ず付いている）を使用する際に必要な数とでも覚えてください。（実際の処理はコンピュータを使用するので関係ないです。）