統計学的画像再構成法である

OSEMアルゴリズムの基礎論

【第1章】確率・統計の基礎

１．６ 条件付き確率

さて、皆さんには競馬などをやったことがある方もいらっしゃるでしょう。どの馬が１着でどの馬が2着なのか、そして配当は・・・。そのドキドキ感が楽しいものです。ここである８頭立てのレースがあって、ども馬も勝つ確率は同じと仮定しましょう。あなたの馬券は「１−４」としましょう。そこに必ず当たる予知能力者があなたの前に現れて、“おまえの買うレースで１番と５番と８番は着外である”と予言しました。さて、この予言があった場合とない場合で、あなたの馬券が当たる確率は変わるでしょうか？

全ての馬は勝つ確率は同じとしました。そこでなにも知らされていないならば、馬番１−４の出る確率は、

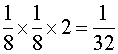
となります。着順が１−４と４−１の2通りがあるから2倍されています。

　今度は予知能力者の情報を事前に知らされたとしましょう。この予言者の予言は必ず当たるので、1番の馬は1着にも2着にも入らないことになります。つまりこのとき、馬番１−４の出る確率はなんと、「０」になってしまうのです。つまり、この場合は、“おまえの買うレースで１番と５番と８番は着外である”という新しい情報を得ることにより、馬番１−４の出る確率が、1/32から０に変わったことになります。

このようにある事象Bが起こったもとでの事象Aの確率を、《 Bが与えられたときのAの条件付き確率 》といい、P(A｜B)と書き、次のように表します。

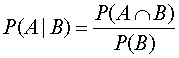
ただし、P(B)＞０の時のみ定義されます。つまり起こりえない情報のもと｛ P(B)=０ ｝では、条件付き確率は定義されません。この式を簡単に説明しますと、P(A｜B)は、AとBが同時に起こる確率を、Bが起こる確率で割った値に等しいということです。

この条件付き確率の考えは、有名な“ベイズの定理”に使用されます。これは確率の話ではあまりにも有名で基本の定理です。ベイズ統計学という1分野が確立されているほど、ベイズという数学者は有名です。