統計学的画像再構成法である

OSEMアルゴリズムの基礎論

【第1章】確率・統計の基礎

１．５離散型と連続型確率変数

　何度も例題といえばコインやサイコロで申し訳ないのですが、またまたサイコロを使って解説していきましょう。(１．３)や(１．４)での説明にあったように、サイコロの出る目は、１、２，３，４，５，６というように、飛び飛びの値をとります。このように飛び飛びの値をとることを離散型といいます。また時間の流れを考えてみましょう。われわれはダイナミック・シンチの検査を行いその結果を見るとき、5分後とか20分後とかの飛び飛びの値を見ることがあります。しかし、時間とは途切れることなく流れています。このような値の取り方を連続型といいます。われわれは連続的にデータ見るときは、タイムアクティビティ・カーブの形などで見ています。連続するデータを絶え間なく、見ていることはできません。連続データには無限に細かくデータが詰まっているのですから。

《離散型の解説》

　さてもう少し数学的に説明しましょう。でも例はサイコロを使います。サイコロを振ってある目がでる確率は1/6でしたね。これをグラフにして見ましょう。

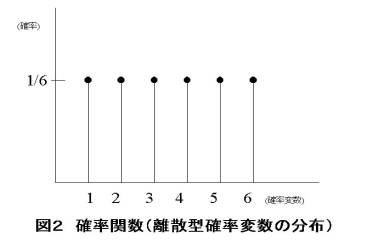
横軸に出る目を書きます。縦軸は確率を書きます。この場合はどの目も同じ確率ですから図のようにつまらないグラフになります。これを式に書いてみると、

となります。これを確率関数といいます。ここで、とは実数のことを表す記号です。たまにRで代用するときもありますのでご注意ください。例えば4の目が出る場合は以下のようになります。

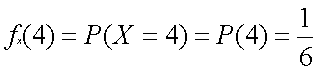
もう一つ、分布関数というのがあります。離散型確率変数の分布関数は次式で表します。

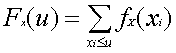
これもグラフにしちゃいましょう。

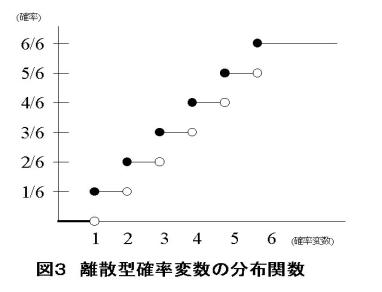
なんか変なグラフですね。これを階段関数とかステップ関数といいます。このグラフの意味することは文字通り、事象の起こりうる確率の分布を表すグラフなのです。細かく見てみましょう。まず横軸の１のあたりに注目しましょう。１のすぐ上に白丸（○）があります。そして○の左に少し太い線が引いてあります。このグラフは離散的ですから、1以下の数値は存在しません。よってこの部分での確率はゼロです。そしてちょうど１のとき、確率は1/6に跳ね上がります。もう少し上に黒丸(●)があります。白丸はその部分は含まない印で、黒丸は含む印です。つまり1以上2未満の確率は1/6ということです。そして２の時にまたまた跳ね上がり今度は確率が2/6になりました。これは2以下がでる確率が2/6ということを表しています。さらに3未満まで確率は同じですから、3未満の確率は2/6ともいえます。でも3未満といっても、サイコロの目ですから、１か２しかないのです。以下同様に考え、6以下の目が出る確率、つまり何らかのサイコロの目が出る確率は１ということです。もちろん、サイコロの角でバランスよくサイコロが立つなんてことは考えていません。

　離散型の分布関数の意味はつまり、起こりうる確率を足しているということで、すべての場合を考慮するとその確率は１（つまり100％）になることを示しています。この性質は連続型でも同様です。

《連続型の解説》

　さて、今度は例を少し難しくしちゃいましょう。でもみなさん見たことのある形です。それは正規分布（またはガウス分布）です。詳細は後で述べますので、よくわからない人もここでは軽く流しちゃってください。図４は正規分布のなかでも基本的な標準正規分布（平均＝０、分散＝１）のグラフです。

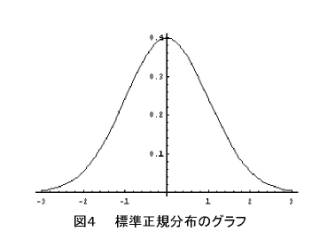
とりあえず説明ために、標準正規分布の式を書いてみます。

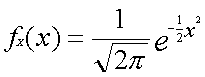
この式の特徴は負の値を取らないことです。また、横軸を正の方向に、また負の方向にどんどん大きくしていっても、グラフはX軸に限りなく近づきますが重なることはありません。そしてこのグラフとX軸とで囲まれる面積を求めると１になります。この全体の面積とは実は離散型と同じように、すべての場合を考慮する確率１と同じことになるのです。面積の求め方は次の式で表します。

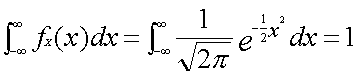
この計算方法はいわゆる高校で習った積分（リーマン積分）では解けません。これをちゃんと解くにはルベーグ式積分という手法が必要です。これは大変難しく、位相数学の概念が必要になります。これをここで簡単に説明ってわけにはいかない（私も専門外！）ので、興味のある方は書店の数学書コーナーへ行って探してください。

　さて、図４のようなグラフは、Xの取りうる値は無限にあります。つまり、グラフは密に詰まっているので数値は連続しています。これを確率密度関数といいます。離散型の確率関数と言い方が違っていますね。連続型にも当然分布関数が存在します。それを以下に示しましょう。

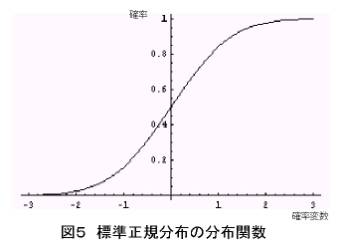
なんか特性曲線みたいなグラフですね。このグラフはX軸の負の方向にどんどん進んでも確率はゼロに限りなく近づきます。そして、正の方向にどんどん進むと確率は１に近づきます。形こと違いますが、離散型の時と共通していませんか？　ここでは離散型と連続型の違いがなんとなくわかっていただければ十分です。