統計学的画像再構成法である

OSEMアルゴリズムの基礎論

【第1章】確率・統計の基礎

１．３ 確率変数と確率分布

　実験をしてみましょう！！　実験といってもなにも特別なことをするわけではないです。何も用意しなくてもいいです。想像で行きましょう。コインの実験とサイコロの実験の２つを考えます。

《コインの実験》

　コインを投げて、表と裏のどちらが出るか、を考えましょう。みなさんやったことありますね？　別に1円玉だろうが500円玉だろうが、はたまた1セントコインでも構わないのですが、このコインは「イカサマコイン」ではないことを保証しておきましょう。また“コインがうまく立つこともあるではないか”などとひねくれた考えは捨ててください。

このときコインは表と裏の2種類しかでません。そこで、ω₁→表、ω₂→裏としてこの集合を

Ω＝｛ω₁、ω₂｝

と書いて、このΩ（オメガ）を標本空間と呼び、ω₁、ω₂などを標本点と呼びます。（注；ωはΩの小文字です。）そして、表と裏がそれぞれ出る確率は当然 です。そこでこの確率をPとして、表と裏が出る確率を

　　　

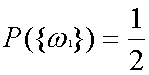
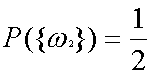
と書きましょう。このとき表がでた回数を考えましょう。このとき表が出たら１を、裏が出たら０を対応させます。そうすれば回数を計算できますね。つまり、ω₁→１、ω₂→０を対応させているわけです。次に“賭け事”をしてみましょう。表が出たら10円､もらい、裏なら10円払います。同様に考えるとこのときは、ω₁→10円、ω₂→−10円を対応させているわけです。つまりこれは空間標本の各標本点にある実数を対応させるような関数を考えているのです。上の実験を以下のように式で書きます。表の出る数の場合の関数をX、賭け事の場合の関数をTとすると、

X(ω₁)=1、X(ω₂)=０、T(ω₁)=10、T(ω₂)=−10、

と書くことにします。このように標本空間の各点に実数を対応させる関数を確率変数といいます。

　ここで確率変数の取りうる値についてその確率の式の書き方考えましょう。つまり、表の出る確率を示す式は、

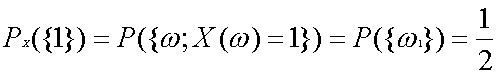
と書くことができます。これは書き方ですから好きな方法で結構です。同様に他の場合をすべて式に書くと同様に

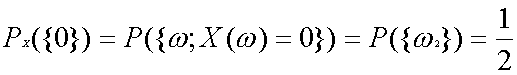
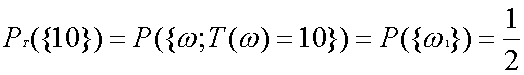
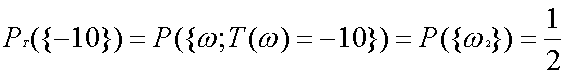
と書けるわけです。次も全く同様ですのでさっと見てみましょう。

《サイコロの実験》

　イカサマのないサイコロを振る実験を考えましょう。このときサイコロの出る目は１、２、３、４、５、６でこれをω₁→１、ω₂→２、ω₃→３、ω₄→４、ω₅→５、ω₆→６と対応させることができます。ここで各目が出る確率は ですから、

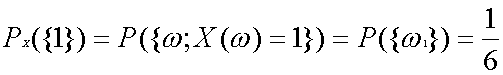
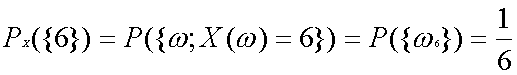
と書けるでしょう。また、サイコロの目が2から５までのどれかが出る確率は、

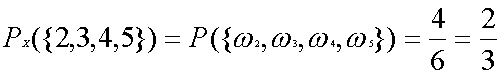
であることはおわかり頂けるでしょう。当然すべての目のどれかが出る確率は、

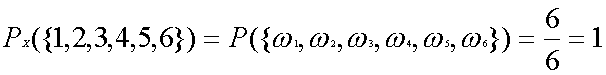
です。確率は１を超えることはありません。もし計算結果が１を超えていたら、それは計算間違いがあります。見直しましょう。

以上をまとめてみましょう。標本空間Ωとその確率Pが与えられているとき、その標本空間の点ωに実数を対応させる関数Y(ω)を確率変数といい、事象A⊂R(実数全体)に対するY∈Aなる確率は、

で与えられる。このようにして得られたP_Yを確率変数Yの確率分布といいます。

この章は記号と言葉の説明ですので、あまり深入りしないように「さらっと」いきましょう。