統計学的画像再構成法である

OSEMアルゴリズムの基礎論

【第1章】確率・統計の基礎

１．２ 平均値（算術平均）と標準偏差

　それでは、いよいよΣの記号を使って平均値の式を考えます。

統計学で大変重要なのに、結構いいかげんになるものがあります。それは、“母数と統計量”です。母数とは母集団分布の様子を表す数値で、パラメータと呼ぶことがあります。ここで母集団とは、調べたい集団の全体を示します。たとえば、日本人男性の平均身長を調べたいとき、実際に存在する約6千万人からの身長を全部測ることはほぼ不可能に近い作業になります。このような集団を母集団といいます。実際は自分で調査できるある地域の数百人とか数千人とかのデータの平均を使って、母集団のそれを推定するわけです。この小さな集団（データを取った集団）を標本集団といいます。もちろん自分で母集団のデータをすべて測れるならそれにこしたことはありません。

　母集団分布の中心位置を示す母数を母平均μ（ミュー）、ばらつき具合を示す母数を母標準偏差σ（シグマ）といいます。これに対し、データからの求めた平均を標本平均(エックス･バー)と書き、標本標準偏差をs（エス）と書き、これらを統計量と呼びます。結構理科系の人でも、この母数と統計量がごっちゃになっている人が多くいますので、みなさんはしっかり区別しましょう。そこで今までの記号を使って平均値の式を示してみましょう。

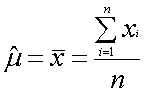
さてここで、μの上に＾（ハット）なる記号がついています。標本平均と母平均は一般に一致しません。誤差を含んでいます。したがって

であるのが普通です。これが母数と統計量の違いなのです。ここで、

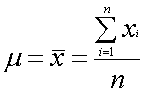
と書いてあったならば、これだけで“この人は統計が理解できていない”とまで言われかねません。特に数学科の出身者はこだわります。次に標本標準偏差について解説しましょう。これも母数と区別するための＾を用いて、

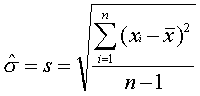
と書きます。さらに、標準偏差を二乗したものを分散と呼んでいます。実際の計算では分散としての値はあまり使用しません。標準偏差で覚えておきましょう。さて、ここで注意したいのは、平均の方はnで割っているのに、標準偏差の方はn-1で割っています。このn-1を“自由度”と呼んでいます。この説明は後で設けます。標準偏差には、nで割るものもありますが、ここではn-1で割るものだと思って結構です。ここで、以下の式を平方和と呼びます。

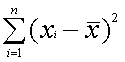
また、こんな性質もありますので覚えておきましょう。非常に重要な性質で、証明にもよく使います。

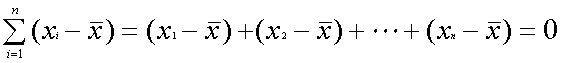
平均を取り扱うことは統計で最も基本的なことであり、最も重要なものです。平均について細かく説明すればいくらでも説明できるほどです。ここではこの程度の内容で終わりにしましょう。この先必要なことは、その都度解説をしていきます。