���v�w�I�摜�č\���@�ł���
OSEM�A���S���Y���̊�b�_
�y��1�́z�m���E���v�̊�b
�P�D�P�R�@�Ŗސ���
�@����Ɩ{���̍Ŗސ���Ƃ������t���o�Ă��܂����D���҂������܂����D���̐߂͂��܂܂ł̒��ōł������C����������e���o�Ă��܂��D������Ă��������D���ꂪ�I���Ƃ��悢��{����MLEM�COSEM�̏͂ł��D
�Ƃ���Łg�ށh�Ȃ鎚�͂��܂茩�����܂���ˁD�g�䂤�h�Ɠǂ݂܂��D�g���ʁh�ł͂���܂���I�I�@���̈Ӗ��́u�����Ƃ��炵���v�Ƃ����Ӗ������ŁC���闝�_�ɂ�蓾��ꂽ�������C�ł��m���炵������ɂ���ē����闝�_���Ŗސ���@�ƌĂ�ł��܂��D�Ȃ�̂��Ƃ��H�ł����C�F����悭�g�����̂ŁC����f�[�^���O���t��Ƀv���b�g���āg���֒����h�������āCR���������L�ӂ��I�@�Ƃ��̌��ʂ�ǂ����܂���ˁD���̒����͍ŏ����@�Ƃ������@�ŋ��߂�̂ł����C������Ŗސ���@��1�ł��D�ł��ߎ��ł��钼���ߎ����ŁC���ʂ�\�z���邱�Ƃ��s���Ă��邩��ł��D�ŏ��ɂ������܂������C��X�����ʂɌv�Z���Ă���g���ϒl�h���Ŗސ���ł��D
�@����1�C�u�j���[�g���@�v�Ƃ����T�O���ȒP�ɉ�����܂��傤�D����͒����ߎ��̊T�O�ł��D���d��ŁC������@�͂��̃j���[�g���@���g���Ă��܂��D
�i�j���[�g���@�j
�@����͒P���Ȍv�Z���J�Ԃ��čs���C�����ߎ��l�Ƃ��ċ��߂���@�ł��DMLEM�Ɠ����T�O�ł��ˁI�I�@���Z�̐��w�ŁC����Ȑ��̐ڐ��̕��������Ă̂�����܂����D������g���܂��D�v���o���Ă��������D����͏ȗ����܂��D
�ŏ��ɂ����f(x)�͔����\�ł���Ƃ��܂��B������
f(x)=0�@
�������j���[�g���@�́A
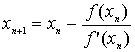 �@�@�@�@�@�@
�@�@�@�@�@�@
�Ə����܂��B������n+1�Ƃ�n�́Ci�Ԗڂ̌v�Z�������܂��D�ŏ��C�܂菉���l��x0�Ƃ��܂��傤�D���̈Ӗ����l���܂��ƁC�㎮�̉E�ӂ͓_(xn,
f(xn))�ɂ�����f(x)�̐ڐ���x���Ƃ̌�_��x���W��\���Ă��܂��D�ŏ���x0���E�ӂɑ�����C�v�Z���ʂ�x1�Ƃ��܂��Dx1���܂��E�ӂɑ�����Čv�Z���C���ʂ�x2�Ƃ��܂��D���l�Ɍv�Z���J�Ԃ��Ǝ���ɉ��ւƋ߂Â��Ă����̂ł��D�}�Ɏ����Ă݂܂��傤�D
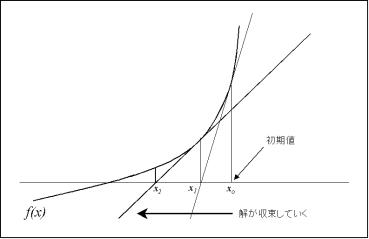
�j���[�g���@�ɂ����̎����̗l�q
���̃O���t�͎��G�g x-2e-x=0
�h�v�Z���ʂ̎����̗l�q�����������̂ł��D�����͂���Ԃ����Z�̉ŁC�����l��x0=1�Ƃ��܂����D�c����xn+1�̒l�ł���Cx1���玦���Ă���܂��D
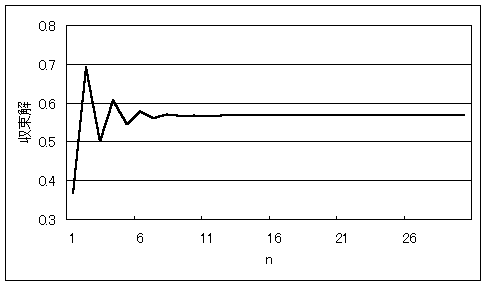
x-2e-x=0�̃j���[�g���@�ɂ����̎���
���̂悤�ɁC�J��Ԃ����Z���s���A�ߎ��������߂���@�𒀎��ߎ��@�Ƃ����܂��B
�@���āC�Ŗސ���ɘb��߂��܂��傤�D�ŏ��ɂ������̒�`�������Ă����܂��D
�y��`�P�z
�W�{X = ( X1,
X2, �c, Xn )�̕��z���p�����g���b�N���f���CP={f(x ;��) :�Ɓ�����R k}�ɑ����Ƃ���Df(x ;��)�͊m�����܂��͊m�����x���Ƃ���D�^����ꂽ�ϑ��lx=(x1,
x2,���, xn)�ɂ���f(x ;��)���C�Ƃ̊��Ƃ݂Ȃ������̂�ޓx���ƌĂсC�Ƃ���L(��; x )�ƕ\���D�܂�C
L(��; x ) = f(x ;��)
�Ƃ���x=(x1,
x2,���, xn)�������_���W�{�̏ꍇ�͂��̖ޓx���́C
![]()
�ŗ^������Dfi(x ;��)�͕�W�c�̊m�����܂��͊m�����x���ł���D
�y��`�Q�z
�ޓx�����ő�ɂ���l�C![]() ���Ŗސ���l�Ƃ����C
���Ŗސ���l�Ƃ����C
![]()
![]() ���Ƃ̍Ŗސ���ʂƌĂԁD
���Ƃ̍Ŗސ���ʂƌĂԁD
�y��`�R�z
�@�ޓx���̑ΐ����Ƃ������̂�ΐ��ޓx���Ƃ����A
log{L(��; x )}
�ƕ\���B�܂��A��=(��1, ���, ��k)��R k�̊J�W���ŁA���ꂼ��̃�i�ɂ��Ă�1���Γ��������݂���Ƃ��A�Ŗސ���l![]() �͈ȉ��̕����������B
�͈ȉ��̕����������B
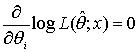 i=1,���, k
i=1,���, k
�����ޓx�������Ƃ����B
���Ē�`1����l���Ă݂܂��傤�D�ςȋL�����o�Ă��܂����C�v�͓Ɨ��������ۂ��l�����ꍇ�C���̖ޓx���Ƃ����̂́C�����̊m���i���x�j�������������̂ł���Ƃ����Ă��܂��D�T�C�R����2���āC2�̖ڂ������ďo�邱�Ƃ́C�m����1/6�~1/6�̂悤�ɁC�e�X�̊m�����|���Ă���̂ł��D���̂��߂ɋL���Ƃ��ă����g���Ă���̂ł��D
��`2�͂Ȃ�ł��傤���H�@����͒�`1�łׂ̂��ޓx�����ő�ɂ���l�����߂邱�Ƃ��Ŗސ���ƌĂт܂��Ƃ����Ă��܂��D�gSup�h�Ƃ́g�ő�́h�Ƃ����Ӗ��ł��D���Ȃ݂Ɂu�ŏ��́v�́uInf�v�Ə����܂��D�O�̋L���́C��W�c�ɑ��ĕW�{�W�c�̃p�����[�^�Ɏg�p����L���ŁC��ʂׂ̈ɗp���Ă���ɂ����܂���D
��`3�́C�����P�ɖޓx���̑ΐ�������������Ȃ̂ł����C���̂��߂��Ƃ����܂��ƁC����ɂ��C�L���������ɒu�������邱�Ƃ��ł���̂ł��D�Ȃ�̂��߁H�@���Ƃł��܂����C�v�Z���ȒP�ɂ��邽�߂̃e�N�j�b�N�Ȃ̂ł��D�����Č㔼�́C����1�K�����������̂��O�ɂȂ邱�Ƃ������Ă��܂��D1�K��������Ƃ́C�ɒl�����߂邱�ƂɂȂ�܂��D�Ⴆ�Ώ�ɓʂ�2�����Ȃ�C�Ȑ�����ԏ�̂Ƃ���ɗ���Ƃ���������Ă��܂��D���Z�̐��w�ł́C���̃O���t���������ɋɏ��_��ɑ�_�܂��ϋȓ_��T�����߂ɔ������g���܂����D�L���u![]() �v�͔�����\���L���ŁC�u�f�B�[�v�Ƃ��u�f���v�Ƃ��u���E���h�v�Ɠǂ݂܂��D�����̏ꍇ�C�u�f�B�[�v�Ɠǂ݂܂��D�]�k�ł����C������w�ŏK�������钆���l�̐��w�̍u�t�́C�u�����_�H�v�Ɣ������Ă��܂����D���̐搶�͑�w����w�@�����呲�Ȃ̂œ��{��̓y���y���Ȃ̂ł����C�u�����_�v�Ƃ͉��ꂩ�킩��܂���ł����H�H
�v�͔�����\���L���ŁC�u�f�B�[�v�Ƃ��u�f���v�Ƃ��u���E���h�v�Ɠǂ݂܂��D�����̏ꍇ�C�u�f�B�[�v�Ɠǂ݂܂��D�]�k�ł����C������w�ŏK�������钆���l�̐��w�̍u�t�́C�u�����_�H�v�Ɣ������Ă��܂����D���̐搶�͑�w����w�@�����呲�Ȃ̂œ��{��̓y���y���Ȃ̂ł����C�u�����_�v�Ƃ͉��ꂩ�킩��܂���ł����H�H
�����̂��Ƃ���C���ϒl���{���ɍŖސ���l�C�܂�ł��m���炵���l�͕��ϒl�ł��邱�ƁC���K���z�ƃ|�A�\�����z�̂Q�̕��z�ɂ��ďؖ����܂��傤�D���������������܂��C���܂܂ł̂��Ƃ�p����ł���͂��ł��D
�i���K���z�̏ꍇ�j
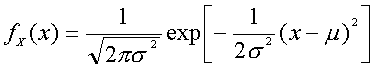
���āC�ޓx���͂ǂ̂悤�ɏ�����ł��傤���D�ȉ��̂悤�ɏ����܂��D
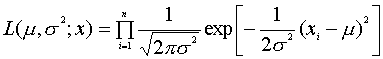
���ɑΐ��ޓx�����l���܂��傤�D����͌v�Z�����₷�����邽�߂ł����D
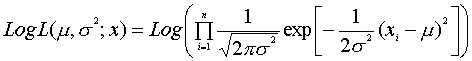
���āC�v���o���܂��傤�DLog�̌v�Z�ł��DLog ab=Log a + Log b �ł����ˁD�܂�Log�̒��̊|���Z�́C�o���o���ɂ��đ��Z�ɒ�����̂ł��D�܂����Z�͈����Z�ɂł��܂����D����Ǝ��̂悤�ɕό`�ł��܂��D
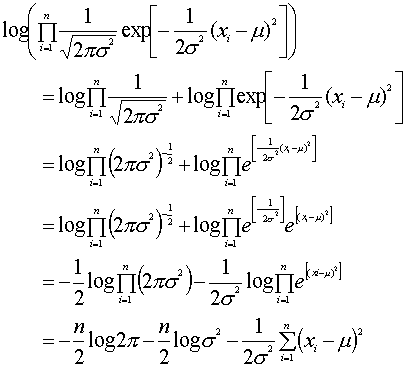
���ɂ��̖ޓx�������͂ǂ��Ȃ�ł��傤�D�����������̂��O�ł����ˁD�p�����[�^�ϒl�Ƃ��܂����̂ŁC�ʂŔ������܂��D����ƃʂɑ��ĉE�ӑ�ꍀ�Ƒ�͒萔�ł�������������0�ɂȂ�܂��D����Ėޓx����������Ȃ��Ȃ�܂��D�]���đ�O���݂̂��l���܂��D����ƁC
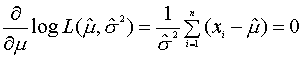
�܂肱�̎�����������̂́C![]() �̂Ƃ��C�܂�W�{�W�c�̕��ϒl�̃p�����[�^�͕�W�c�̕��ϒl�Ɉ�v���邱�ƂɂȂ�܂��̂ŁC�Ŗސ���l�͕��ϒl�Ɉ�v���܂����D���U�Ɋւ��Ă͓��l�Ƀ�2�Ŕ�������Ƌ��܂�܂��D�ŏI�̎����������Ǝ��̂悤�ɂȂ�܂��D�m���߂Ă݂Ă��������D
�̂Ƃ��C�܂�W�{�W�c�̕��ϒl�̃p�����[�^�͕�W�c�̕��ϒl�Ɉ�v���邱�ƂɂȂ�܂��̂ŁC�Ŗސ���l�͕��ϒl�Ɉ�v���܂����D���U�Ɋւ��Ă͓��l�Ƀ�2�Ŕ�������Ƌ��܂�܂��D�ŏI�̎����������Ǝ��̂悤�ɂȂ�܂��D�m���߂Ă݂Ă��������D
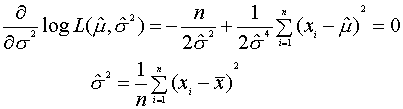
�����Ŕ����́C�Δ����ƂȂ�̂ł����C�ׂ������Ƃ͏ȗ����܂��āC�����Ƃ��Ă��܂��̂ł��������������D
�i�|�A�\�����z�̏ꍇ�j
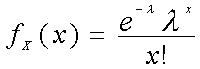
���l�ɍl���Ă݂܂��傤�D������̓p�����[�^���P�i�Ɂj�����Ȃ��̂ŁC�����y�ł��D���Ď菇�́C�ޓx�������C���̑ΐ����Ƃ����ΐ��ޓx�����쐬���C�������ɕύX���������܂��D������p�����[�^�Ŕ����������̂��O�ƂȂ�ޓx���������l���Ă�����Ŗސ���l�����߂��܂��D�ł͂���Ă݂܂��傤�D
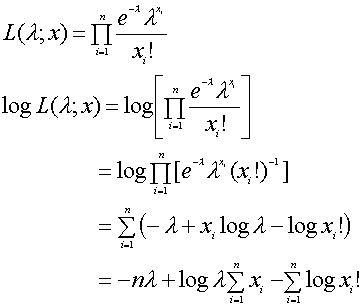
�ɂŔ������܂��D
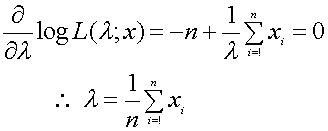
�Ō�̎��́Cn�̃f�[�^��S��������n�Ŋ����Ă���C�܂蕽�ς��v�Z���Ă��܂��D�܂蕽�ς����߂邱�Ƃ��|�A�\�����z�̃p�����[�^�ł��镽�ςƈ�v���܂����D
�@MLEM�ł悭������Ŗސ���ɂ���ĉ������߂���̂��E�E�E����͂܂蕽�ϒl�����߂邱�Ƃ��C�ł�����炵�����l�ł���I�@���Ă��Ƃ��C���_�I�Ɏ������̂ł��D�ł����狹���ĕ��ϒl���C�ł��M�p�������鐔�l�Ƃ��č̗p�ł���̂ł��D���ϒl�̐M�����́C�f�[�^�������ق������̐��x�������Ȃ邱�Ƃ͌o���I�ɂ��킩��܂����C���v�w�I�ɂ����̂Ƃ���ł��D
_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/
����ő�1�͂͏I���ɂ��܂��D���͗Տ��Ɏg���Ă���MLEM��
�T�O�ɓ���܂��D�悭����ΊȒP�Ȃ��Ƃ�����Ă���̂ɋC������
�v���܂��D���Z�́u�����E�|����E����v��3���J�Ԃ��Ă��邾��
�ł��D�{���ł��D�����Z�͍s���܂���I�I
�Ō�ɁC���I�ȓs���ɂ��C
���s���x��܂������Ɛ[�����l�т������܂��D
���ꂩ�����낵�����肢�������܂��D
_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/