統計学的画像再構成法である

OSEMアルゴリズムの基礎論

【第1章】確率・統計の基礎

１．１２　ポアソン分布

量子力学は、古典力学では説明できないことは皆さん技師学校や短大，大学などで習いましたね。（もう忘れましたか？）量子力学での概念、つまり量子の世界は確率で物事を考えて構成されています。ポテンシャルエネルギーがどうしたこうしたとか，を考えるとき、波動方程式は確率の概念に則っています。

さて、ポアソン分布とはどんなときに使うものなのでしょうか？これはある事象が起こる確率が、低いような事象に対して成り立つような分布なのです。光子の発生は、原子レベルで見ると確率は低いものなのです。従って我々が扱う光子（主にγ線）が発生する確率は、ポアソン分布に従っているのです。飛行機事故なんかも実はポアソン分布に従っている（めったに起きないものでしょ！！）のです。ではポアソン分布の定義を示しましょう。

（定義）

　確率変数Xが次の確率関数をもつとき、Xはパラメータλ（＞0）のポアソン分布に従うという。

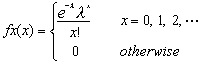
ポアソン分布は二項分布の特殊例であり、二項分布の期待値と分散が等しい場合となる。

つまり、E(X)＝Var(X)＝λである。

さてポアソン分布にはとても重要で，特殊な性質があります．ML-EMの説明に特に重要な性質を示していきましょう．

ポアソン分布は期待値λだけであらゆる値が求められるため、個々の確率や標本の大きさについてほとんどわからなくても平均値さえわかれば、「まれに起こる現象」を表せるので非常に有用な性質があります。つまり平均値さえわかれば分布の形がわかるのです．これは計算するのにとても便利です．ポアソン分布はどんな形をしているのでしょう．λを変化させたグラフをいかに示します．

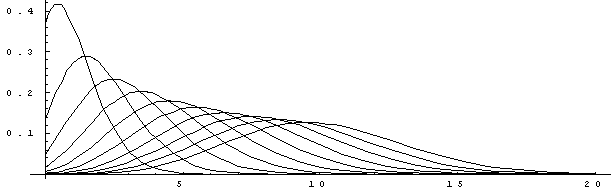
図　λ=1〜10まで変化させたときのポアソン分布

λが小さい場合はグラフの形が左右非対称なんですが、λを大きくなると左右対称に近づき、良く知られている正規分布（かなり幅広ですが）に近づいていくことがわかります。次に画像再構成理論の構築に関連して、非常に重要な２つの性質について述べましょう。

【分布の減算】

ポアソン分布に従う関数（あるいは現象）をP₁(x), P₂(x),・・・, P_n(x)とします。するとこれらの和

P(x)＝P₁(x)＋P₂(x)＋・・・＋P_n(x)

もまたポアソン分布に従います。しかし、減算を行うともはやこの性質は保てないのです。すなわち、

P(x)＝P₁(x)−P₂(x)

はポアソン分布といえる保証はもはやなくなってしまいます。

【ポアソン分布の再生性の定理】

　X₁, X₂, ･･･, X_nが独立でそれぞれのパラメータλ_i, i=1,2,･･･, nのポアソン分布に従うとき、S= X₁＋X₂＋･･･＋X_nはパラメータλ₁＋λ₂＋･･･＋λ_nのポアソン分布に従う。

じつはこのよく解らないような定理が，ML-EMの最も重要な基本式を求めるのに利用される性質なのです。第2章では実際にこの定理を使って，なにがどうなって使われているのかを説明と，証明をします。この証明には，始めにやったΠや�狽ﾌ記号の意味，対数計算などが必要になります。結構，高等数学っぽいですよ。お楽しみに！！