統計学的画像再構成法である

OSEMアルゴリズムの基礎論

【第1章】確率・統計の基礎

１．１１　正規分布

　正規分布またはガウス分布とも呼ばれている分布の1つで，皆さんも良く聞く名前かと思います．それもそのはずで，自然現象の多くがこの正規分布に従っています．身長や体重といったものから製品のばらつき具合など，実に多くのものが適合します．放射線の話では，誤差の分布や，最近話題のマルチスライスCTのZ軸（体軸）方向にかけるフィルターの近似関数にも使われています．ではどんな分布なのでしょう．早速定義を示します．

【定義】

　確率変数Xが次の確率関数をもつとき、Xはパラメータμ、σ²の正規分布に従うという。

ただし、−∞＜μ＜∞、0＜σ

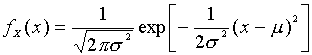−∞＜ x ＜∞

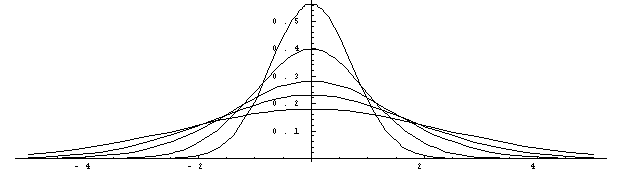
図　μ、σを変化させたときの正規分布

μは母数の平均値，σ²は母数の分散を示します．図の上のグラフは，μを一定にし，σ²を変化させた時のグラフです．σ²を大きくするとグラフは横に広がった形になります．下のグラフは，μを０から1に変化させ，σ²を同様に変化させたグラフです．どのグラフの左右対称です．決して正規分布は左右非対称にはなりません．またこれらの性質から，正規分布はμとσ²の二つのパラメータで形が変化することがわかります．そしてもう1つ重要な性質として，正規分布に従う集合同士を足しても引いても，その集合は正規分布の性質を保つのです．この性質は次に示すポアソン分布と異なる性質で，計算やモデルの組み立てに重要な性質なのです．

　正規分布にはさらにもう1つ，重要で面白い性質があります．これを標準正規分布といい，ある変換を行うと，どんなパラメータの正規分布も，μ＝0，σ²＝1　の正規分布になるのです．以下に示しましょう．

【標準正規分布】

Zが標準正規分布に従うならばZの確率密度関数は、

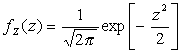　　　　−∞＜ z ＜∞

である。このときZは以下で表すことをZ変換と呼ぶ。

つまり，z＝〜〜　の式に変数Xを代入して計算されたzの集合の分布を考えると，不思議なことにμ＝0，σ²＝1　の正規分布になるのです．これもなにかと便利な性質です．

正規分布と次節のポアソン分布は，MLEMを考える際に重要です．特にポアソン分布は“肝”になりますから，よく覚えておきましょう．これら分布の説明のあとに最尤推定の概念を解説し，実際に正規分布とポアソン分布を用いてMLEMに適合できる基礎の部分の証明と理論を示します．分布の式をよく覚えておいてください．またLogや��，Πの計算がでてきます．忘れたかたは復習しておきましょう．