統計学的画像再構成法である

OSEMアルゴリズムの基礎論

【第1章】確率・統計の基礎

１．１０　二項分布

さてこれから本格的に数学ですので、いきなり数式から入ります。数式に弱い方・・・気を失わないように！！

二項分布とは、確率変数Ｘが次のような確率関数fx(X)を持つとき、Xはパラメータn、pの二項分布に従うといいます。

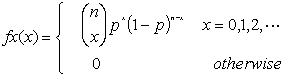
ここでnは正の整数で、pは0≦p≦1とします。

<<< NOTE >>>

さてここで、式の中に，nとpが入ったカッコはなんなのかを解説しましょう。知っている方はもちろん飛ばして下さい。高校の数学で、確率の勉強をしたことがある人は、“順列”、“組み合わせ”って習いませんでしたか？このカッコは“組み合わせ”を表しています。そしてもう一つ、“！”の記号の意味も解説します。これは“階乗”というものでした。

【階乗とは】

適当な正数をnとします。nの階乗を、n！と書いてその意味は、

n！＝n×(n-1) ×(n-2) ×・・・×３×２×１

です。つまりnから一つづつ数字を下げて、１になるまでの全部の数字を掛けるということです。

5！＝５×４×３×２×１＝120　ということです。

【順列とは】

適当な正数をn、r (r≦n)とします。n個の異なるものの中から、異なるものr個を取り出して順番に並べるような操作を順列といい、_nP_rと書きます。たとえば、１円玉、10円玉、50円玉、100円玉が１枚ずつあって、この中から２枚を選んで並べるには、何通りの並べ方があるのでしょうか？実際にやってみても良いのですが省略して、答えは12通りです。これを記号で書いて、₄P₂＝4×3＝12となります。一般には、

_nP_r＝n×(n-1) ×(n-2) ×・・・×(n−r＋1)　または　_nP_r＝n！／(n−r)！

となります。確かめてみて下さい。

【組み合わせとは】

例として，順列と同じコインを使用します。記号は、_nC_rと書きます。順列は並べることについて考えました。組み合わせは、単に選ぶ事のみを考えます。つまり、順列では１円玉・10円玉の並びと、10円玉・1円玉の並びは違うものだったのですが、組み合わせでは２枚の組のみを考えることになるので、（１円玉・10円玉）と（10円玉・1円玉）は同じものになります。すると４枚のコインから２枚を選ぶ組み合わせは・・・6通りですね。これを記号で書くと、₄C₂＝4×3／2×1＝6となります。一般には、

_nC_r＝n！／r！(n−r)！　または　_nC_r＝_nP_r／r！

となります。これも確かめてみて下さい。

では二項分布の話しに戻りましょう。今まではサイコロやコインの話ばかりでしたので、放射線に関する例でこの分布を考えてみます。

線源弱係数をμとすると、光子が厚さdの吸収体を透過する確率pはよくご存じの次式で表せます。

pは確率だから、d＝0（厚さ0）のときに1になります。では通過しない確率はどうでしょうか。全確率が１だから、１から通過する確率pを引いた値になりますね。つまり(1−p)＝1−e^-μdです。これを二項分布の式に当てはめると、n個の光子が厚さdの吸収体を通過する確率分布は以下の二項分布の確率関数に従うことになります。

では二項分布とはどんな分布なのでしょう．グラフにするとこんなグラフです．

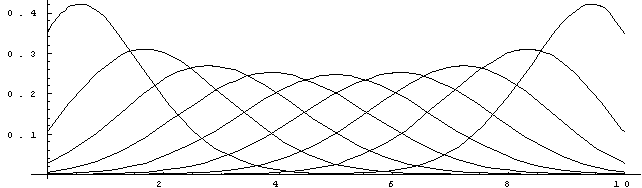
図2.2　 n=10 , p=0.1〜0.9まで変化させたときのときの二項分布

このグラフは，nを10に固定して，pを0.1〜0.9まで0.1刻みで変化させたときのときの二項分布です．一番左の曲線がp=0.1になります．p=0.5のとき左右対称なグラフになっています．二項分布の平均と分散はそれぞれ，平均がnp、分散がnp(1−p)となります．

また注目すべきは、二項分布の式でn＝1のとき組み合わせ値は1なので、二項分布の式がベルヌーイ分布の式と一致します。つまりベルヌーイ分布は、二項分布の特殊例ということになります。

　次はポアソン分布です．いままでの分布とポアソン分布は“つながり”があります．またML-EMの説明にはポアソン分布が登場します．