���v�w�I�摜�č\���@�ł���
OSEM�A���S���Y���̊�b�_
�y��1�́z �m���E���v�̊�b
�P�D�P �V�O�}�i���j�ƃp�C�i���j�Ƒΐ��iLog�j�̋L��
���āA���ϒl�����������ڂ����L���Ō��Ă݂܂��傤�B�u���ςȂ�ĊȒP����I�v�@�܂��A�������킸�ɏ��������`���Ă��������B���ϒl�ɂ͂���������܂��B�݂Ȃ��悭�g�����ϒl�Ƃ́g�Z�p���ς܂��͑������ρh�Ƃ������̂ł��B���̑��Ɂg���ς܂��͑��敽�ρh�A�g���a���ρh�ȂǂƂ��������̂�����܂��B���ꂩ��Z�p���ςɂ��ĉ�����܂��B
�������A���̐���������O�ɂ��ꂩ��b�����e�ɂ͖����ɏo�Ă���A���i�V�O�}�j�̋L���K���܂��傤�B���Z���w�̐���ŏo�Ă����L���ł��B
���̋L���͈ȉ��̂悤�ȈӖ��������܂��B
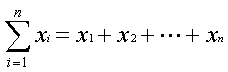
�܂�x1����xn�܂ł����ɑ������Ƃ��Ӗ����Ă��܂��B�����Ax2����x7�܂ł𑫂��̂ł���Ȃ��
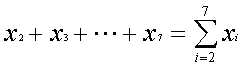
�Ə����܂��B�����Ĉȉ��̂��Ƃ�a��n�����Ƃ��Ӗ����܂��̂ŁA
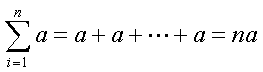
�Ɩ��܂��傤�B�悤����ɇ��Ƃ́A��������̋K�����̂��鑫���Z���A�_���_�������̂͂߂�ǂ������̂ŁA���ꂢ�ɂ������悭�������߂̋L���ł��B
������悭�g���L����������܂��B����͉~�����Ŏg�����i�p�C�j�̑啶���ŁA���Ə����܂��B����͍��Z�Ŏg���܂���̂ŁA�����ł�������o���܂��傤�B���͑����Z�̋L���ł������A���͊|���Z�̋L���ł��B�܂�A
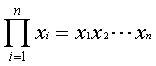
�@�Ə����܂��B����͊��ς܂��͑��敽�ς̂Ƃ��Ɏg�p���܂����A�Ŗސ���ɂ���������o�Ă��܂��B�ȏ�̋L���͍Ŗސ�����w�Ԃ̂ɃC���b�ĂقǏo�Ă��܂��B����Ă��܂��ƂĂ��֗��ȋL���ł�����s����Ȑl�͂�����đ�������܂��傤�B
���ꂩ�����1�A���Z���̎��ɐ��w�����ɂȂ�l�̑����́A���̋L�������̂悤�ł��B����́A�ulog�v�ł��B�Ŗސ���̍ŏ��ɂ���log���g���܂��B��������������܂��傤�B���̎������Ă��������B
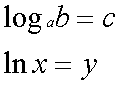
��̎��́Aa��c�悵����b�A�ɂȂ邱�Ƃ�\���Ă��܂��B����a�̕�������Ƃ����܂��B���̂Ƃ�����10�̂Ƃ�����p�ΐ��Ƃ����Ae�̂Ƃ������R�ΐ��Ƃ����܂��Be�͐��l�Ƃ��Ă�2.7���炢�ie
=2.71828182---�j�Ɗo���Ă����܂��傤�B���R�ΐ��̂Ƃ��́A���̎��̂悤�ɋL���鎖������܂����A��ʓI�ɒ�̕����������ĂȂ���Ώ㎮�̋L�ڂł����R�ΐ��Ɣ��f���܂��B�ł͖��ł��B
�y��z�@![]() ��
��![]() �͂����ł��傤���H
�͂����ł��傤���H
�@�@�@�@�����5�����悵����25�ɂȂ邩�ƕ����Ă���̂ł�����A�ȒP�ł��ˁB
�����́u2�v�ł��B
�@�@�@�@�����āA����e�����悵����e�ɂȂ邩�ƕ����Ă���̂ł�����A
�����́u1�v�ł��B
�ȉ��ɑΐ��̐����������܂��B�����ł��̂Ŋo�����ق��������ł��傤�B�ŏ��̌����͓��ɏd�v�ł��I�ꂪ�����ĂȂ���Ύ��R�ΐ��ł��B
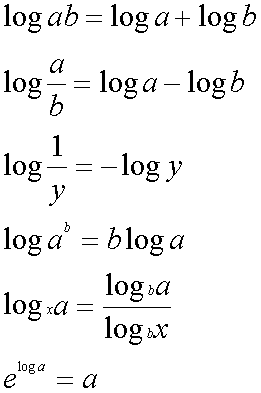
���w�ɂ͐F�X�ȋL������������o�Ă��܂����A����Ă��܂��Ε֗��ŊȒP�Ȃ��̂ł��B���Ȑl�͌J��Ԃ����Ă��������āA����Ă��������B���̋L���̈Ӗ��Ɋ���邱�Ƃ�������ǂ��Ă������Ƃ̊�{�ł��B���w�͌v�Z���ł���E�ł��Ȃ��ł͂���܂���B���w��Ƃ������t�ƕ��@�ŁA�Ȋw�I���ۂ�������Ă��邾���ł��B���w�҂͏ł炸�������ǂ��Ă��������B